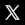XV. Dette publique
Causes de la dette publique
Le tableau suivant montre que la dette publique brute augmente plus vite dans les pays développés que dans les pays émergents. Dans les premiers, la dette moyenne sur la période 2001-2022 est de 94 % tandis qu'elle est de 46 % dans les pays moins riches.
Deux possibles relations causales sont :
l'endettement public stimule le développement économique, dans la mesure où l'endettement sert à financer des infrastructures (routes, énergie, ...) et services (enseignement, justice, ..) qui stimulent le développement économique ;.
- le développement économique stimule l'endettement public ("on ne prête qu'aux riches").
Ces relations causales sont peut-être liées dans une boucle de rétroaction.
Mais (au moins) un autre facteur détermine le niveau des dettes publiques : les crises économiques. Ainsi dans le tableau suivant nous avons retiré les deux périodes de crise de cette période :
la crise des subprimes de 2008-2009, annoncée par des études "prédictives" favorables au secteur bancaire, qui via son officieux lobby qu'est le FMI, a réussi à convaincre les décideurs politiques que si les États ne lui achetaient pas massivement des produits financiers pourris, le système bancaire mondial s'effondrerait ;
la crise de la covid-19, annoncée par des études "prédictives" favorables au secteur pharmaceutique, qui via son officieux lobby qu'est l'OMS, a réussi à convaincre les décideurs politiques que si les États ne lui achetaient pas des millions de vaccins conçus à la va-vite (durée moyenne avant AMM réduite d'un facteur 18 !), cela provoquerait des millions de morts sur la planète, après d'atroces souffrances (étouffement).
Et si on supprime également les années 2010 à 2012, durant lesquelles la crise initiée en 2008-2009 a continué à faire sentir ses effets, la tendance générale de l'évolution des dettes publiques devient orientée à la baisse !
Le mythe de la sécurité sociale "intenable"
Depuis le début du 21° siècle, l'augmentation des dettes publiques n'est donc pas du tout causée par la sécurité sociale, mais par une "logique" délétère de maximisation des profits dans les secteurs bancaire (cf. ./creation-monetaire#systeme-bancaire) et pharmaceutique.
Dans ces deux cas (subprimes et covidisme), ces "crises" ont été l'occasion de massifs transferts financiers publics vers de grandes entreprises privées (bancaires et pharmaceutiques), "justifiés" par la "nécessité" quasiment existentielle de prévenir une "catastrophe mondiale à venir". Dans un cas comme dans l'autre, celle-ci s'est finalement réalisée, mais uniquement par des effets pervers de prophéties autoréalisatrices. Ainsi les prétendus prémisses, qui ont nourri la médiatisation de messages catastrophistes, n'étaient pas constatables dans la vie de tous les jours, mais uniquement via le business de "l'information". Ces "crises" ont donc clairement un caractère systémique, lié au contrôle non démocratique des moyens de production, en l'occurrence : de la science, de l'information, de la monnaie et des médicaments.
On notera à cet égard, que les trois secteurs économiques où l'on observe le plus de condamnations judiciaires, notamment pour corruption, sont dans l'ordre : 1. finance ; 2. pharmacie ; 3. énergie [source]. Malheureusement, il n'y a ni condamnations à des peines de prison fermes, ni nationalisations punitives, de sorte qu'il est hautement probable que les montants des amendes sont inférieurs aux revenus des activités sanctionnées ...
Dépenses et recettes. Si l'on détaille l'analyse, en termes de dépenses et recettes publiques (⇒ solde public ⇒ dette publique), on constate que :
- les périodes de crises économiques correspondent logiquement à une hausse des dépenses et une baisse des recettes publiques ;
- l'augmentation tendancielle des dettes publiques résulte du fait que les recettes des États ont tendance à augmenter moins que leurs dépenses. Ainsi dans le graphique suivant la pente de la droite de tendance des dépenses (0,21) est plus de deux fois supérieure à celle des recettes (0,9).
La fraude fiscale et les paradis fiscaux jouent donc un rôle important dans l'augmentation des dettes publiques.
Évolution des recettes et dépenses publiques (économies avancées, % du PIB)
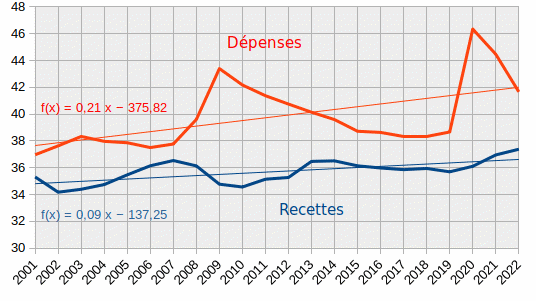
Source : FMI tableur : recette-depenses-publiques.ods.
Équilibre
La dette publique est l'accumulation des emprunts engagés par l'État pour financer les soldes publics annuels lorsque ceux-ci sont négatifs. Les soldes publics annuels sont donc les flux qui augmentent (solde négatif) ou diminuent (solde positif) le stock que constitue la dette publique. Le solde public est négatif – on parle alors de déficit, qui augmente la dette – si les dépenses de l'État (dont les intérêts sur la dette ...) sont supérieures à ses recettes (essentiellement constituées des impôts). Lorsque le solde public est positif on parle de capacité de financement, et s'il est négatif de besoin de financement ou de déficit
Pour équilibrer son budget, l'État dispose théoriquement de divers moyens :
- à effet immédiat :
- diminution des dépenses publiques ;
Cependant l'effet à plus long terme sera négatif si cette réduction concerne l'investissement plutôt que la consommation publique ⇒ baisse du potentiel de croissance du PIB ⇒ baisse des recettes fiscales (PS : mais selon les économistes libéraux, même les dépenses publiques d'investissement ne sont pas la meilleure solution, car via leur financement par la fiscalité ou l'emprunt, elles rendraient plus coûteux l'investissement par le secteur privé (effet d'éviction), que les économistes libéraux considèrent comme plus productif par nature).
- augmentation des recettes fiscales, par augmentation du niveau et/ou de l'assiette des taux fiscaux ;
Cependant l'effet à plus long terme peut être négatif si la hausse de la pression fiscale provoque un ralentissement économique tel que les recettes fiscales diminuent "in fine".
- emprunter le solde négatif au secteur privé (entreprises et ménages nationaux ou étrangers) ou à d'autres États ou à sa Banque centrale ;
N.B. Il y a création monétaire avec effet inflationniste si (i) l'emprunt est fait auprès du secteur bancaire national (BC + banques commerciales), (i) et que l'emprunt sert à financer la consommation plutôt que les investissements. Cet effet inflationniste est cependant annulé (ceteris paribus) lors du remboursement de l'emprunt au secteur bancaire.
- diminution des dépenses publiques ;
- à effet retard : stimuler la croissance économique (ce qui accroît les recettes fiscales et réduit les dépenses de chômage) en améliorant l'efficacité (notamment par simplification des procédures et neutralisation de la corruption) :
- du système juridique et législatif ;
- du système financier ;
- du système de formation ;
- du système de R&D.
Pourquoi les États n'empruntent-ils pas sans intérêt auprès de leur Banque centrale
La réponse de la doxa libérale atlantiste est que cela inciterait les gouvernements à mener des politiques budgétaires inflationnistes. Cependant ce raisonnement ne tient pas la route. Si l'État a la rigueur de se soumettre au paiement d'intérêts, pourquoi n'aurait-il pas la rigueur de s'imposer des conditions quantitatives et qualitatives à ses emprunts auprès de sa BC, lesquelles conditions garantiraient le caractère non inflationniste de ces emprunts, tout en économisant le paiement d'intérêts !? La véritable raison de la politique actuelle n'est-elle pas le pouvoir de corruption des décideurs politiques par le lobby bancaire, principal bénéficiaire des charges d'intérêt de la dette publique ?
Patrimoine
public net
Analysons enfin la valeur du patrimoine net (actifs-passifs) de l'État, selon le type d'administration (centrale, locale, SS). La valeur du patrimoine net des administrations centrales est généralement (fortement) négative, car elles portent l’essentiel de la dette publique, tandis que celle des administrations locales est généralement largement positive, car elles détiennent l’essentiel des actifs non financiers. Enfin, celle des administrations de sécurité sociale est généralement positive [exemple de la France].
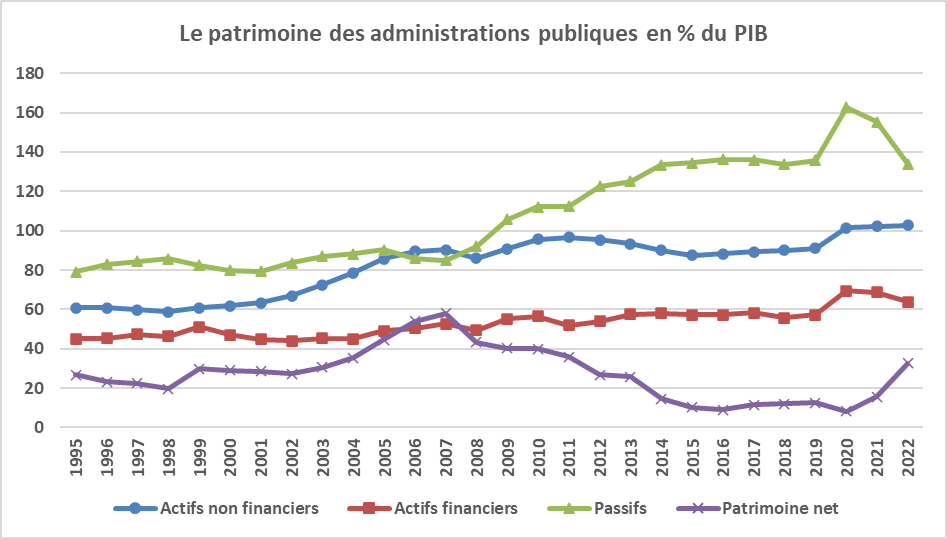
Le graphique suivant montre que malgré une dette publique élevée, le patrimoine public net (c-à-d moins la dette) demeure positif.
Dynamique
Nous avons vu que l'État peut se financer par les impôts, des emprunts, les dividendes d'entreprises publiques (celles-ci étant de plus en plus rares...), ou encore la création monétaire (NB : ces deux derniers moyen sont limités par des contraintes de redistribution et d'inflation, respectivement).
Concernant l'emprunt, la pérennité de l'État, ainsi que sa puissance économique et politique, lui permettent d'obtenir des prêts (en provenance du secteur privé national et étranger, ainsi que d'États étrangers) à des taux très inférieurs à ceux appliqués aux ménages et entreprises privées. La raison en est que les obligations d'État sont moins risquée que des obligations privées, et encore moins que des actions d'entreprises privées : approfondir : /principes-monetaires#determinants-des-taux-interet.
Nous allons ici modéliser la dynamique des relations entre dette publique, solde budgétaire, croissance du PIB et taux d'intérêt. L'objectif est de déterminer le niveau de solde budgétaire que le gouvernement doit respecter s'il souhaite stabiliser la dette publique, étant donné le taux de croissance du PIB et le niveau des taux d'intérêts.
Soient :
- Gt les dépenses (hors charges d'intérêt) et Tt les recettes de l'État pour l'année t ;
- Dt , St et SPt : la dette, le solde budgétaire et le solde primaire (c-à-d hors charge d'intérêts, c-à-d avant prise en compte de ces charges d'intérêts), de l'année t ;
- yt = Yt / PIBt : ratio d'une variable quelconque Yt en proportion du PIBt ;
- rt, gt, it : le taux d'intérêt de la dette publique et les taux de croissance du PIB et des prix, gt = gRt + it le taux de croissance nominal (c-à-d en valeur) du PIB (gRt étant appelé taux "réel").
Taux d'intérêt de la dette publique. La dette publique est financée par des obligations émises par l'État auprès d'investisseurs nationaux ou étrangers (banques, assurances, fonds de pension) mais aussi (dans certains pays) auprès de la Banque centrale. Ces obligations sont émises régulièrement (les emprunts d'État), à des taux et échéances qui peuvent varier à chaque émission. Par conséquent la gestion de la dette est complexe. On peut cependant calculer chaque année le taux effectif de la dette publique en divisant les charges d'intérêts payées annuellement, par le montant de la dette de l'année précédente : rt = chargest / dettest-1 ⇔ charges t = rt * dettest-1.
Le solde primaire, c'est les recettes moins les dépenses (hors charges d'intérêt) de l'État :
SPt = Tt - Gt ⇒ (1)
- si Tt > Gt ⇒ SPt > 0 : le solde primaire est un excédent ;
- si Tt < Gt ⇒ SPt < 0 : le solde primaire est un déficit.
N.B. Un déficit est par définition un solde négatif. Mais dans le langage courant (notamment des journalistes), on utilise aussi bien "déficit de 3%" que "déficit de -3%" pour exprimer un "solde de -3%" ou encore "solde déficitaire de 3%". Heureusement, la notation mathématique est quant à elle sans ambiguïté.
Le solde budgétaire est le solde primaire dont on retire les charges d'intérêt :
St = SPt - rt * Dt-1 (2)
- St < SPt
- si rt = 0 ⇒ St = SPt
Le solde budgétaire est un flux qui s'ajoute annuellement au stock que constitue la dette, qu'il réduit donc s'il est positif, et augmente dans le cas contraire :
Dt = Dt-1 - St(3)
On peut exprimer Dt en fonction de SPt en substituant St de (2) dans (3) ⇒
Dt = Dt-1 * ( 1 + rt ) - SPt (4)
Enfin en divisant les équations (2) à (4) par PIBt = PIBt-1 * ( 1 + gt ) on obtient leurs formes en ratios relativement au PIB :
st = spt - rt * dt - 1 / ( 1 + gt ) (5)
dt = dt-1 / ( 1 + gt ) - st (6)
dt = dt - 1 * ( 1 + rt ) / ( 1 + gt ) - spt (7)
Lecture intuitive de ces équations :
- (5) : rt diminue le solde budgétaire tandis que gt l'augmente ;
- (7) : rt augmente la dette tandis que gt la diminue.
- il suffit dans (7) de poser rt=0 et d'alors remplacer spt par st pour retrouver (6) ;
- (6) exprime dt en fonction de st ⇒ rt n'y apparaît pas, tandis que (7) exprime dt en fonction de spt ⇒ rt y apparaît.
Solde
stabilisant
Calculons maintenant la valeur que le solde budgétaire doit atteindre pour que la dette diminue :
dt / dt - 1 < 1 ⇔ à partir de (6) :
1 / ( 1 + gt ) - st / dt-1 < 1 ⇔
st > - dt-1 * gt / (1 + gt )
(8)
Approximation : gt étant généralement petit relativement à 1,on peut omettre le dénominateur, de sorte que la condition de réduction de la dette est approximativement st > - dt-1 * gt. Ainsi par exemple si la dette est de 100% du PIB (dt-1=1) et que le PIB augmente de 2% (gt=0,02) alors la dette diminue si le solde budgétaire est supérieur à -2%. Donc même avec un solde budgétaire négatif de -1.9% la dette décroît !
Calculons maintenant la valeur que le solde primaire (c-à-d avant déduction des charges d'intérêt) doit atteindre pour que la dette diminue. Il suffit de substituer (5) dans le membre de gauche de (8) :
spt - rt * dt - 1 / ( 1 + gt ) > - dt-1 * gt / (1 + gt ) ⇔
spt > - dt-1 * ( gt - rt ) / (1 + gt )
(9)
Approximation : on peut évidemment faire la même approximation que pour le solde avec charges d'intérêt, de sorte que la condition de réduction de la dette est approximativement spt > - dt-1 * ( gt - rt ). Ainsi par exemple si l'on reprend les mêmes conditions que ci-dessus et que :
- le taux d'intérêt rt = 1 % ⇒ il faut st > - ( 0,02 - 0,01 ) = - 1 %
- le taux d'intérêt rt = 3 % ⇒ il faut st > - ( 0,02 - 0,03 ) = 1 %
Ainsi, dans les conditions ci-dessus, la hausse du taux d'intérêt de 1% à 3% requiert des économies budgétaires d'au moins 1% - (-1%) = 2% du PIB pour réduire (ou au moins stabiliser) la dette publique.
Politique
budgétaire
S'il est relativement facile pour un gouvernement d'agir sur le solde public primaire, il lui est par contre beaucoup plus difficile (voire impossible à court terme) d'influer substantiellement sur :
- gt ... et cela d'autant plus que l'économie est ouverte ;
- rt ... du moins lorsque ce taux d'intérêt de la dette publique est déterminé par le marché plutôt que par la Banque centrale.
Soulignons enfin que les critères que nous venons de déterminer ne démontrent aucunement qu'il existerait un niveau de dette publique qui serait optimal du point de vue économique (comme il existe une température optimale du corps humain). Ils exposent seulement quelles mesures un gouvernement devrait appliquer pour maintenir la dette publique à un niveau déterminé.
Critères de Maastricht
2. Nuisibilité
Définition et motivations
Les critères de Maastricht (1992), qui constituent le fondement de la politique économique de l'Union européenne, interdisent (*) aux pays membres notamment d'avoir une dette publique supérieure à 60% du PIB et un solde budgétaire inférieur à -3% du PIB [source1, source2].
(*) Il s'agit d'un interdiction implicite car en pratique il s'agit de faire converger les dettes vers le niveau de 60%.
N.B. Le ratio déficit/PIB est de type flux/flux, tandis que le ratio dette/PIB est de type stock/flux.
Il est fondamental de comprendre que les critères de Maastricht sont une condition de viabilité de l'union monétaire. Or, appliquer une union monétaire à des pays aussi différents que l'Allemagne et la Grèce est un non sens macroéconomique ! (cf. /principes-monetaires#union-monetaire-europeenne).
Au niveau microéconomique des coûts des transaction de change, ceux-ci sont devenus quasiment nuls, car la monnaie est essentiellement électronique et où l'affichage électronique des prix en devises étrangères se généralise (étiquettes électroniques et applis de conversion visuelle sur téléphone mobile).
D'un point de vue théorique aussi bien que pratique, on ne peut affirmer l'existence d'un niveau optimal absolu de la dette publique. En particulier il n'a jamais été démontré que les critères de Maastricht seraient des valeurs économiques naturelles, à l'instar de la gravitation en physique. La dynamique analysée dans la section précédente dit seulement qu'une dette à 60% et un solde budgétaire à -3% cela correspond à un taux de croissance nominal du PIB de 0,03 / 0,6 = 5%. Rien d'autre !
Les critères de Maastricht ne sont pas des critères économiques mais politiques. En 1995 la dette moyenne des 12 pays signataires du Traité de Maastricht était d'environ 77% du PIB, tandis que les dettes publiques allemande, française et anglaise étaient respectivement de 55%, 55% (idem pour les USA) et 45% [source]. Il est donc plus que probable que ce pourcentage a été choisi parce qu'il était proche de celui de l'Allemagne et de la France, les leaders économiques et politiques de l'UE [source].
On soulignera enfin que, loin de converger vers le niveau de 60 % de leur PIB, les dettes nationales de l'UE ont au contraire divergé ...
Dette publique en % du PIB
Nuisibilité
Déficit. Le ratio de 3% du PIB, imposé aux États par le traité de Maastricht, peut avoir un effet négatif dans la mesure où le déficit peut financer des dépenses d'investissement (y compris en capital humain : formation, R&D, santé, ...). Or s'il est logique que les dépenses de fonctionnement soient financées par prélèvements obligatoires, il est tout aussi logique que les investissements le soient par emprunts publics. Autrement dit, en terme de ratios de solde (et de dette) public on ne peut traiter également ces deux types de dépenses : contrairement aux dépenses de fonctionnement les investissements en capital (matériel comme humain) génèrent de la croissance économique et donc une capacité de remboursement des emprunts.
- Il convient d'autre part de vérifier si, comme il devrait, le montant du déficit est bien augmenté des amortissements.
- Si les retraites des fonctionnaires sont comptabilisées "hors bilan", ce qui est le cas notamment en France, le ratio dette/PIB diminue de plusieurs dizaines de points de PIB. [source].
Dette. Quant à la limite de 60 % du PIB imposée par le Traité de Maastricht est d'autant plus absurde que la dette considérée es la dette brute c-à-d la somme des passifs sans déduction des actifs [source]. Raisonner sur base de la dette brute revient à passer sous silence que la dette publique permet notamment de financer des investissements produisant un patrimoine public (écoles, routes, hôpitaux, ...), qui participent au développement économique, lequel générera des revenus permettant de rembourser les emprunts publics.
NB : en France environ un tiers du patrimoine public est financier.
Il convient donc de comparer la dette brute (la somme des passifs) au patrimoine (la somme des actifs). On obtient alors une toute autre image de la situation. Ainsi le graphique suivant montre que le patrimoine net (actifs- passifs) est positif ! (mais la situation se détériore depuis la crise des subprimes de 2007-2008, les État s'étant endettés – pour sauver des banques privées mal gérées (*) – ce qui a eu pour effet que la croissance du passif a dépassé celle des actifs.
(*) Et cela alors que toute l'idéologie libérale considère que les entreprises privées sont plus efficaces que les entreprises publiques parce que les entreprises privées qui sont mal gérées disparaissent ! Autrement dit, l'idéologie libérale, c'est "faites ce que je dis, pas ce que je fais" !
N.B. En comparant la dette brute au patrimoine on compare deux stocks, alors que le ratio dette/PIB compare un stock à un flux.
Mesures
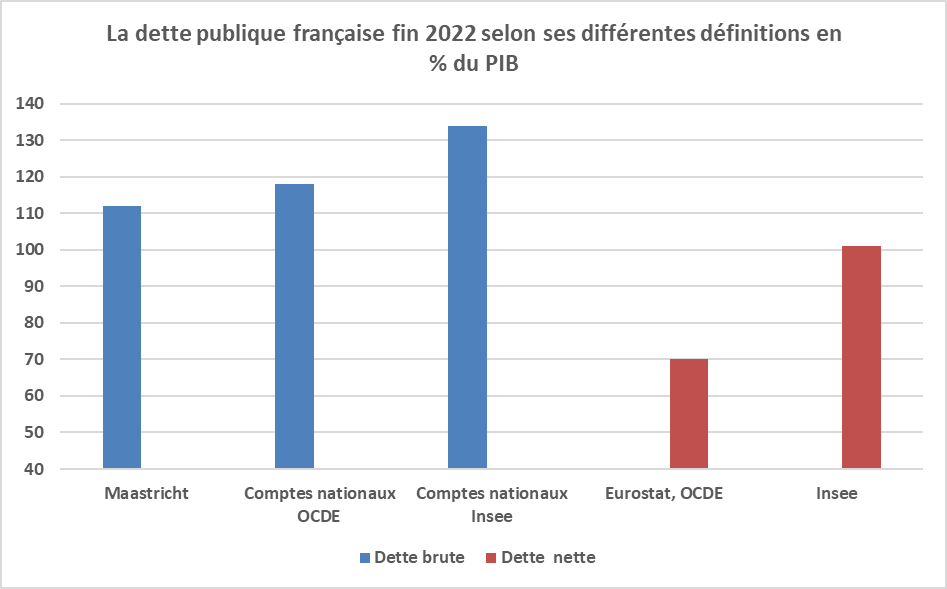
Le graphique suivant (France 2022) montre que la dette publique peut varier du simple au double selon que l'on prend en compte la dette nette ou brute, et dans chaque cas, selon les éléments pris en compte ou au contraire ignorés.
Le calcul de la dette brute peut varier selon (i) qu'elle est consolidée ou non, (ii) qu'elle est calculée en valeur faciale/nominale ou valeur de marché, (iii) que sont pris en compte ou pas certains passifs tels que les engagements de retraite de l’Etat envers ses agents (USA, pas UE), etc.
Le calcul de la dette nette des actifs publics peut varier selon que l'on déduit ou pas les actifs non financiers, les actifs financiers tels que actions & parts de fonds d’investissement, etc.
Publique vs privée
2. Personne physique vs morale
3. Public + Privé = National
4. Dette publique : un cas particulier
Introduction
Deux questions en guise d' introduction :
- Pourquoi les décideurs politiques et les entreprises "d'information" nous parlent-ils toujours de la dette publique et quasiment jamais de la dette privée ?
- Pourquoi les agences de notation financière n'appliquent-elles pas aux États le même ratio que pour les entreprises privées à savoir le rapport entre dette et valeur actualisée des revenus futurs ?
Le juteux business de la notation financière
La crise de 2008 fut notamment provoquée par le fait que les agences de notation financière ont accordé la cote maximale de qualité (AAA) à des titres et émetteurs "pourris". D'autre part force est de constater que le business modèle de la notation financière est celui du racket par chantage réputationnel. Il suffit en effet à une agence de notation de publier un rating dévastateur sur une organisation (entreprise ou État) qui ne le mérite pas, pour forcer celle-ci à devenir "cliente" afin de rehausser sa note. Cette stratégie est d'autant plus facile à appliquer que le marché de la notation financière est un oligopole (trois entreprises, toutes états-uniennes, contrôlant 95% du marché) au sein duquel des ententes sont facilement organisables. Selon nous il convient donc, soit de supprimer toutes références aux agences de notation dans la réglementation prudentielle du secteur financier, soit de responsabiliser les agences de notation en les obligeant à se convertir en sociétés d'assurance contre le risque de dévaluation d'actifs financiers, et à réglementer celles-ci plus efficacement (cf. le rôle des CDS dans la crise de 2008). Mais la cause des causes est l'appât du gain privé, de sorte que la solution la plus efficace est d'instaurer la démocratie directe puis de concurrencer les banques privées par des banques publiques (cf. democratiedirecte.net/entreprise-publique).
Personne physique vs morale
Le secteur public est ce que le secteur privé (qui est composé de personnes physiques et morales) décide (plus ou moins démocratiquement) de mettre et faire en commun. Il s'agit d'un acte politique auquel seules les personnes physiques (les individus) devraient participer, sans quoi il y a des effets de "double comptage".
Or, en pratique, on constate que des personnes morales (entreprises et associations) y participent également. Cela pose question lorsqu'on se rend compte du rôle déterminant joué par les grandes entreprises privées dans les décisions politiques (cf. European Round Table), car ces entreprises privées sont la propriété de personnes physiques, qui bénéficient par conséquent d'un pouvoir politique supérieur à la majorité des citoyens.
Autrement dit, cette superposition des droits politiques des personnes physiques (individus) et morales (organisations, privées ou publiques) induit un "effet doublon" dès lors que les organisations ne fonctionnent et n'existent que par les personnes physiques qui la constituent. Ces doublons posent la question du caractère démocratique ou non de la gouvernance des organisations privées comme publiques, c-à-d in fine du contrôle démocratique des moyens de production.
Dans une démocratie directe les entreprises publiques pourraient être gérées sous statut de coopératives publiques.
On pourrait certes objecter que la distinction entre personnes physique et morale conduit à une "double taxation" des entreprises et de leurs propriétaires, favorisant ainsi la redistribution des richesses. Le problème est qu'entre cette théorie fiscale et la réalité la marge est grande (paradis fiscaux, ingénierie fiscale, etc).
Parties prenantes. La problématique est encore plus complexe que cela. Une entreprise implique au moins quatre types d'individus/ménages : actionnaires, employés, clients, fournisseurs. Par exemple une hausse des cotisations patronales peut inciter l'employeur à réduire l'emploi ...
Il convient donc de ne pas confondre dette publique et dette nationale, la première n'étant que la composante publique de la seconde :
Dette nationale :- dette publique (État) ;
- dette privée :
- entreprises ;
- ménages.
Public + Privé = National
Au sein d'un pays (c-à-d une "économie nationale") on distingue donc trois agents économiques : l'État (le secteur public), les entreprises et les ménages (le secteur privé). Par conséquent évaluer la situation d'une économie nationale en se fixant sur la santé financière du seul secteur public – comme le font la plupart des journalistes et politiciens – est absurde.
Ainsi la valeur d'une monnaie nationale ne dépend pas que de la situation financière du secteur public, mais également du secteur privé (entreprises et ménages). Cela doit être interprété au regard des faits suivants :
- au niveau mondial, c-à-d d'une économie "fermée", le montant des dettes est égal à celui des créances ;
- au niveau d'une "économie ouverte" (ce qui est le cas de tous les pays, mais à des degrés divers), il importe de prendre en compte également la position extérieure, qui est l'accumulation des soldes annuels de la balance des capitaux, et donc le stock de créances et de dettes nettes d’un pays à l’égard du reste du monde.
Le tableau suivant montre que l'explosion de la dette nationale US durant la seconde moitié du 20° siècle ne fut pas le fait de l'État mais bien du secteur privé, et en particulier des entreprises financières.
Composantes de la dette nationale US (%PIB)
| 1957 | 2007 | |
|---|---|---|
| État (fédéral) | 75% | 80% |
| État (municipal) | 20% | 20% |
| Entreprises non financières | 45% | 90% |
| Entreprises financières | 5% | 150% |
| Ménages | 45% | 120% |
| Total | 190% | 460% |
[Source p.157]
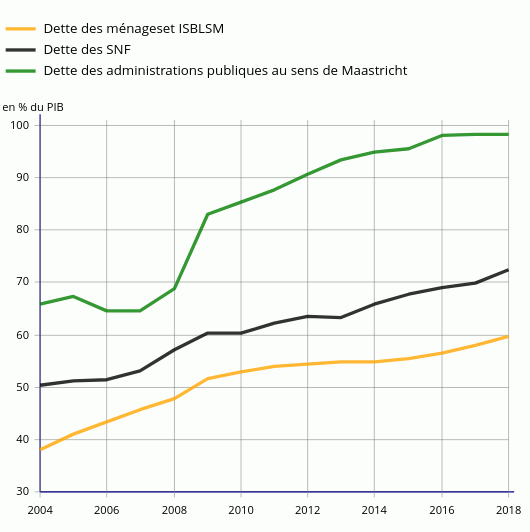
En France, la dette privée représente de façon assez constante environ 1,3 fois la dette publique. Le graphique montre également l'impact délétère de la crise financière initiée en 2007-2008, au profit du secteur bancaire.
Enfin, n'oublions pas que l'endettement peut servir à financer deux types de dépenses : consommation et investissement. Ce qui nous mène à la section suivante ...
Dette publique : un cas particulier
Une dette publique de 60% du PIB (≈ revenu national) signifie que pour rembourser sa dette en une fois un État devrait consacrer 60% de la production annuelle du pays par l'ensemble des agents économiques (État, entreprises et ménages).
Mais plutôt que de comparer le volume de la dette publique (un stock) au PIB (un flux), ne serait-il pas plus pertinent de le comparer au patrimoine économique national (un stock, qui en France représente environ huit années de revenu national : cf. /comptabilite-nationale#patrimoine) ?
Nous allons voir que ce type de raisonnement, consistant à comparer le niveau de la dette à celui du PIB ou du patrimoine, s'il peut être pertinent dans le cas d'une entreprise privée (chiffre d'affaire ⇔ PIB, et actifs de l'entreprise ⇔ patrimoine économique national), il l'est par contre beaucoup moins voire plus du tout dans le cas d'un État.
Ainsi les économistes libéraux aiment évoquer un supposé risque de "faillite de l'État" (défaut de paiement), par analogie avec les faillites d'entreprises privées. Mais cette analogie n'est pas fondée car, l'État dispose de moyens de financement souverains :
- les impôts ;
N.B. Le rendement de l'impôt peut cependant diminuer au fur et à mesure qu'augmente le taux d'imposition, notamment suite à l'échappement fiscal (cf. courbe de Laffer).
- la création monétaire.
N.B. Le recours à la "planche à billets" est cependant limitée par le risque inflationniste. Dans l'Union européenne elle est théoriquement interdite, sauf pour céder aux lobbies bancaire (cf. crise des subprimes) ou pharmaceutique (cf. covidisme), avec la complaisance des gouvernements.
D'autre part, contrairement aux banques, l'État est réellement "too big too fail", car il doit garantir la fourniture de services publics que le secteur privé n'est pas disposé ou en mesure de fournir de façon équitable et éthique. Contrairement aux entreprises privées, la nature de l'État est intrinsèquement collective : alors que l'objectif premier des entreprises privées est la maximisation du profit de ses seuls propriétaires, celui de l'État est de maximiser le rapport qualité/prix des biens & services fournis par lui à la collectivité, et dans une logique de service public (absence de publicité, de technologisme ou encore d'obsolescence programmée).
Il reste évidemment à déterminer quel système politique et économique permet à l'État d'assumer au mieux cette fonction. Nous avons développé la thèse selon laquelle il s'agit de la démocratie directe (cf. democratiedirecte.net/definition) et de l'économie mixte (cf. democratiedirecte.net/entreprise-publique).
L'État constitue donc le champs institutionnel (politique, juridique et économique), pérenne, sur lequel opèrent des entreprises (privées et publiques) en concurrences. La non pérennité des entreprises privées comme publiques (faillites des moins performantes) garantit l'efficacité et la résilience du système (*), tandis que le cadre institutionnel préserve sa stabilité.
(*) Une entreprise, même bien gérée, peut disparaître suite à un changement de paradigme technologique rapide et imprévisible.
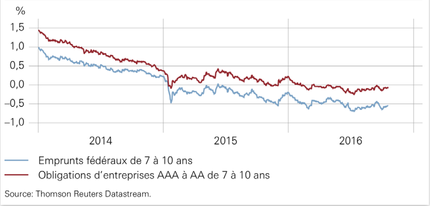
Il en résulte que la durée de vie d'un État est théoriquement infinie ou en tout cas est nettement supérieure à celle d'une entreprise privée et (encore plus) d'un particulier. Cette durée de vie infinie constitue une garantie de remboursement pour les créanciers de l'État (les institutions financières, ménages et autres États détenant les obligations émises par l'État emprunteur), ce que confirme le fait que le taux d’intérêt des emprunts d’État est inférieur à celui des dettes des entreprises privées (cf. graphique ci-dessous) .
Performance de l'État
Quel est l'effet d'une hausse de la dette publique sur la croissance économique ?
Une réponse théorique consiste à distinguer les deux voies de l'endettement public :
- hausse des dépenses publiques :
- allocations sociales ⇒ relance de la demande, à court terme ("stabilisation automatique") ;
- investissements (infrastructure, enseignement, recherche, ...) ⇒ relance de la production, à plus long terme ;
- baisse des impôts ⇒ stimule le secteur privé, à court terme.
Le lecteur aura remarqué qu'il n'y a là que des effets positifs. Mais est-ce le cas dans la réalité ? Les études empiriques apportent une réponse mitigée, mais qu'il importe d'interpréter avec prudence en raison de la complexité des phénomènes économiques, et de biais idéologiques et pressions politiques qui corrompent une partie substantielles des études scientifiques. C'est particulièrement le cas lorsque des simulations de modèles économétriques sont présentées abusivement comme des analyses empiriques. La confusion est d'autant plus aisée lorsque les deux approches expriment leur résultat au moyen du même indicateur : le multiplicateur (des composantes) de la dette publiques sur la croissance économique.
Un professeur d'université pris en flagrant délit d'enfumage
Dans un article intitulé "Le modèle social français n’est pas soutenable", un professeur d'université nous explique qu'en 2021, la Suède présente un ratio dépenses publiques / PIB plus de 12 points inférieur au ratio français (Suède 46,6 %, France 59,05 %), tout en étant capable de produire des dépenses publiques par habitant d'un niveau équivalent à la France. Or il s'agit là d'un raisonnement fallacieux, dont le principe est le suivant :
PIB / hab =
( PIB / X ) / ( hab / X ) =
( X / hab ) / ( X / PIB )
Le professeur utilise alors ce ratio comme une mesure d'efficacité de l'État dans la production de biens & services publics X pour l'ensemble de la population. Sauf que, vous l'avez compris, X peut signifier n'importe quoi : un service public ... ou encore l'investissement par les entreprises privées. Le professeur dit seulement, de façon complexe, que le PIB/hab de la Suède est supérieur à celui de la France. Cela n'est pas étranger au fait que la Suède bénéficie de ressources naturelles importantes : bois, hydroélectricité et mines de fer ...
Conclusion. Les développements algébriques tels que ci-dessus sont certes très utiles pour modéliser mathématiquement une thèse. Il y a cependant abus (grave) lorsque cette modélisation illustrative est présentée aux lecteurs peu avertis comme une démonstration mathématique de la thèse, ce qu'elle n'est pas !
Multiplicateur
De nombreuses études économiques empiriques visent à mesurer/calculer une effet multiplicateur (ou un effet d'éviction, en cas de valeur négative) des dépenses publiques et/ou des impôts sur le PIB. Une définition possible du multiplicateur est :
Δ g t , t+n = Multiplicateur * Δ E t où :
- Δ g t , t+n = augmentation du taux de croissance moyen du PIB de la période t à t+n, induite par Δ E t
- E =
- si multiplicateur "des dépenses publique : Dépenses publiques / PIB ;
- si multiplicateur "fiscal" : Impôts / PIB ;
- si multiplicateur "budgétaire" : Solde budgétaire / PIB = ( Dépenses publiques - Impôt ) / PIB.
Ce multiplicateur peut être positif ou négatif (dans lequel cas on parle alors d'effet d'éviction), et le signe peut changer selon que l'on considère le court ou long terme.
Ainsi un multiplicateur budgétaire de 0,2 signifie qu'une hausse (/baisse) du déficit budgétaire de 1% du PIB durant l'année t se traduirait par une augmentation (/baisse) de 0,2 point de pourcentage du taux de croissance moyen du PIB de la période t à t+n.
Une étude publiée en 2012 par Auerbach et Gorodnichenko suggère que le multiplicateur budgétaire serait habituellement proche de 0 mais grimperait à 2,5 en période de récession [source]. Une étude du FMI publiée en 2013 identifie quant à elle un multiplicateur plutôt constant et légèrement supérieur à 1 [source].
Selon une étude de l'OCDE publiée en 2015, le multiplicateur budgétaire serait positif pour autant que la dette publique ne dépasse pas un certain niveau, qui serait d'environ 80% du PIB pour les pays les plus développés et environ 40% du PIB pour les pays émergeant. Au délà de ces limites la dette exercerait un effet d'éviction sur le PIB via une hausse des taux d'intérêt [source].
Par un heureux "hasard", la valeur limite pour les pays de la zone euro serait d'environ ... 60%, soit exactement la valeur imposée par les critères de Maastricht ! Cette étude tombe donc à point nommé, alors que les critères de Maastricht sont de plus en critiqués pour leur absence de fondement scientifique ...
Ça tire donc dans toutes les directions. Ainsi une étude du FMI publiée en 2012, identifie un multiplicateur de la dette publique, selon lequel la croissance à long terme serait diminuée de 0,2 point lorsque la dette publique augmente de 10 points de PIB [source1, source2].
Quant aux multiplicateurs fiscaux ils seraient de l'ordre de 2-3 : suite à une baisse d'impôt d'un point de pourcentage du PIB, le PIB augmente de 2 à 3% au bout de 3 ans. Thomas Grjebine explique que pour les économistes keynésiens, une baisse d’impôt provoque une augmentation du PIB plus que proportionnelle – on parle de multiplicateur fiscal. Il s’agit d’un cercle vertueux où la baisse d’impôt, en engendrant une hausse du revenu disponible, entraîne une augmentation de la consommation, qui se traduit par des revenus supplémentaires pour les vendeurs, et donc des rentrées fiscales en plus, etc. Cette baisse d’impôt aura un impact positif d’autant plus important que les ménages ont une forte propension à consommer, c’est-à-dire consomment une part importante de leurs revenus (c'est particulièrement le cas de la TVA et de la taxe foncière), et que le pays est peu ouvert au commerce international – l’argent n’est pas utilisé pour acheter des produits importés. Enfin, selon la théorie dite "d'équivalence ricardienne", qui stipule que ce n'est pas le revenu disponible mais le revenu permanent qui détermine la demande, baisser les impôts sans baisser de façon équivalente les dépenses publiques peut n’avoir aucun effet si les ménages, anticipant une hausse future des impôts pour rembourser la dette publique, choisissent d’épargner plutôt que de consommer ces ressources supplémentaires. Les études empirique infirment cependant la validité de cette théorie [source].
Dans un article publié en 2010 les économistes américains Carmen Reinhart et Kenneth Rogoff suggèrent que lorsque la dette publique d'un pays excède 90 % du PIB, ses performances économiques s'en trouveraient amoindries [source]. Cependant selon une étude réalisée en 2014 par le FMI l'existence d'effets de la dette publique sur la croissance économique au-delà d'un certain seuil n'est pas établie, on peut seulement observer que les pays présentant un niveau d'endettement élevé mais dont la dette est en diminution présentent des performances économiques similaires à ceux dont le niveau d'endettement est faible [source].
Les résultats des études varient donc considérablement selon le référentiel (PIB, IDH, ...).
D'autre part :
- dans quelle mesure les valeurs observées des multiplicateurs sont-elles (ou pas) stables :
- dans le temps ? (ou n'est-ce que la valeur d'un phénomène passé, que l'on ne peut extrapoler à aujourd'hui et encore moins à demain ?) ;
- dans l'espace ? (le multiplicateur mesuré dans un pays correspond-il à celui mesuré dans les autres pays ?).
- corrélation n'est pas causalité :
- si une étude empirique suggère une corrélation négative entre dette publique et croissance économique encore reste-t-il à déterminer si c'est la dette publique qui freine la croissance ou si un ralentissement économique provoque une augmentation de la dette publique (il est probable que la causalité soit biunivoque --> il faut alors déterminer quelle causalité l'emporte sur l'autre) ;
- si une autre étude contradictoire suggère cette fois une corrélation positive entre dette publique et croissance économique encore reste-t-il à déterminer si c'est la dette publique (plus précisément les dépenses publiques) qui entraîne la croissance ou si c'est au contraire la croissance économique qui autorise plus de dépenses publiques (et à nouveau, il est probable que la causalité soit biunivoque --> il faut alors déterminer quelle causalité l'emporte sur l'autre).
- la pertinence du PIB comme indicateur de développement économique durable est de plus en plus remise en question [cf. /production#PIB-qualitatif].
Analyse
qualitative
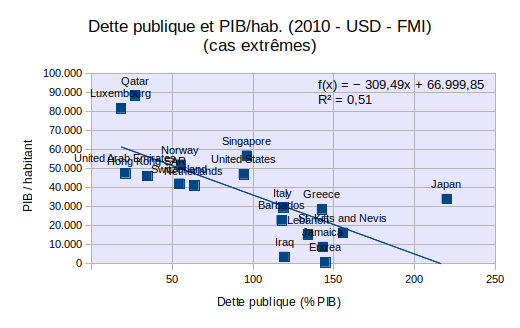
Existe-t-il une corrélation entre niveau de développement et dette publique ? Pour répondre à cette question, nous avons mesuré la corrélation entre dette publique par habitant et PIB/hab, sur base d'un échantillon de 194 pays. L'analyse suggère l'absence totale de corrélation.
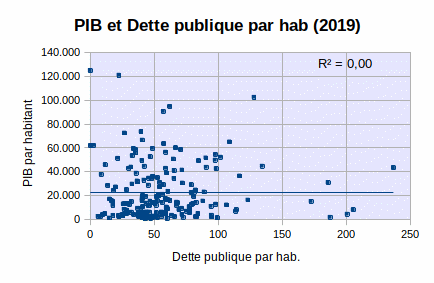
Tableur : dette-publique-et-PIB.ods, source : FMI
Si l'on ne sélectionne que les cas extrêmes (troisième feuille du tableur), dont soit le PIB/habitant est supérieur à 40.000 USD/an (neuf pays), soit la dette publique est supérieure à 100% du PIB (neuf pays), alors on obtient une droite de régression à pente négative, et R2 = 0,51. Ainsi pour les cas extrêmes une dette publique élevée est corrélée avec un faible PIB/habitant. Mais, cette corrélation ne dit rien sur le sens d'une éventuelle causalité : PIB élevé (bas) ⇔ dette publique basse (élevée).
Cependant le graphique suivant (source : UNDP, 2012) révèle une flagrante corrélation entre dépenses publiques passées et l'Indice de Développement Humain (IDH, calculé sur base de l'espérance de vie, de la durée de scolarisation et du revenu brut par habitant), ce qui renforce fortement la thèse que les dépenses publiques stimulent le développement économique.
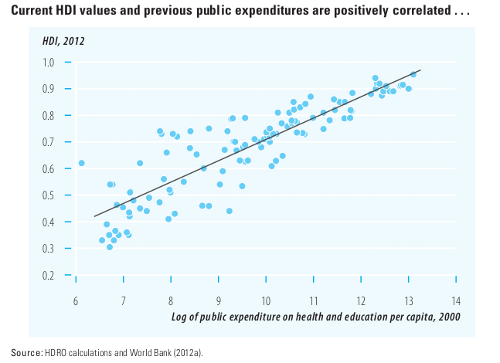
Source : undp.org
Particularités nationales
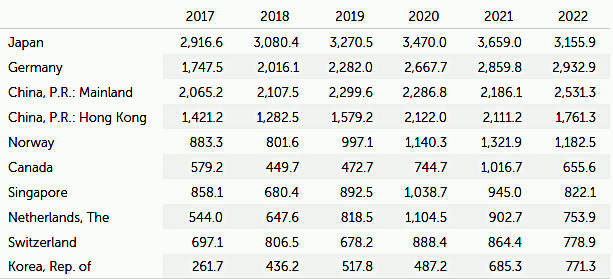
À la question de savoir jusqu'où on peut laisser grimper la dette publique, Jean Tirole, Prix Nobel d'économie 2014, répond en ces termes (pour le moins ambigus) : « si les économistes s'accordent sur les caractéristiques qui déterminent si une dette est soutenable et sur le fait qu'un surendettement est dangereux pour le pays, il est difficile d'identifier de façon précise le niveau maximal d'endettement » [source, p.366]. Il faut donc procéder au cas par cas : nous allons voir qu'au Japon une dette publique de plus de 200% suscite peu d'inquiétude, tandis que l'Argentine s'est retrouvée en grande difficulté avec une dette publique de seulement 60%.
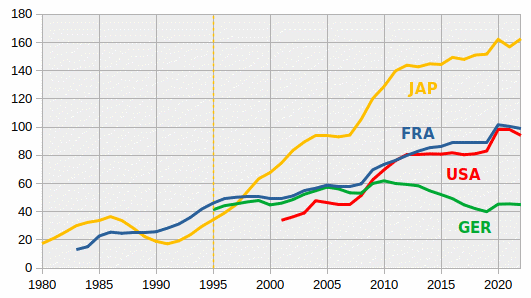
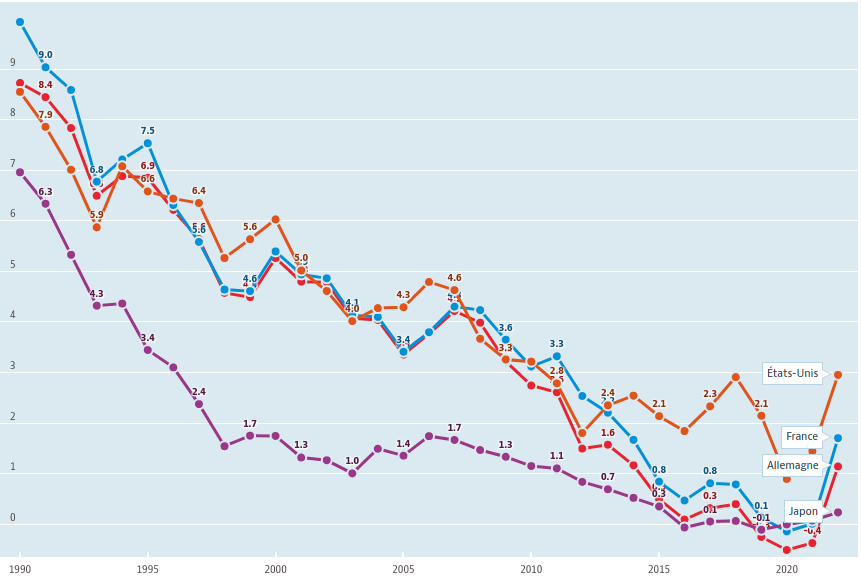
Le graphique suivant, qui montre l'évolution de la dette publique de quatre pays développés, révèle sur la période 1980-2022 :
- le décrochage (vers le haut) du Japon, à partir de 1995 ;
- le décrochage (vers le bas) de l'Allemagne à partir de 2010.
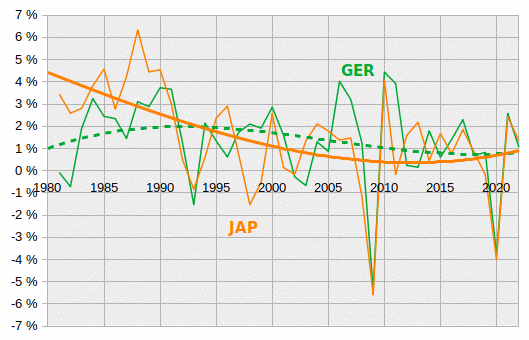
Force est aussi de constater que c'est à partir de cette même année 1995 que la croissance du PIB/hab japonais s'est brusquement infléchie, ... mais pour se stabiliser à une moyenne de 0,7 % par an. Or durant les 27 années depuis 1995, la dette publique du Japon a continué de croître, sans que cela impacte la croissance de son PIB par habitant. La comparaison avec l'Allemagne sur les douze années depuis 2010 est éloquente à cet égard : alors que le différentiel des dettes publiques s'est élargi en "défaveur" du Japon, le différentiel de croissance du PIB/hab s'est rétréci en faveur du Japon (cf. courbes de tendance dans le graphique ci-dessous).
Au travers du cas du Japon, nous allons voir que la notion de bonne/mauvaise dette relève moins du quantitatif que du qualitatif (c-à-d la nature des recettes insuffisantes et des dépenses excessives). Il importe notamment de prendre en compte :
- la part de la dette publique nationale détenue par des agents économiques étrangers ;
Détenteurs de la dette publique. La dette publique est généralement détenue par des sociétés d'assurance, des banques et des particuliers, nationaux ou étrangers (et dans ce dernier cas il peut en outre y avoir des gouvernements étrangers).
- la situation financière du secteur privé (ménages et entreprises) ;
la situation patrimoniale globale du pays vis-à-vis de l’extérieur, mesurée par la position extérieure nette (différence entre le stock d’actifs qu’un pays détient à l’étranger et l’ensemble du passif détenus par les étrangers) : l'endettement du pays fait "effet de levier" si les investissements du pays à l'étranger rapportent plus que le coût de la dette ;
Ne pas confondre la "position extérieure", qui est un stock d'actifs financiers, et la "balance des paiements", qui est un flux d'actifs financiers.
- une Banque centrale accommodante, c-à-d qui prête à l'État à taux d'intérêt faible voire nul, pour financer une politique de développement.
Le niveau élevé des dettes publiques japonaise et belge illustrent qu'un pays peut-être performant malgré (ou grâce à ?) une dette élevée. Au contraire le cas de l'Argentine montre qu'une faible dette publique n'est pas un gage de stabilité économique.
Japon
La dette publique nette du japon est d'environ 160 % du PIB (2022), et le gouvernement anticipe, sans s'inquiéter outre mesure, qu'elle pourrait atteindre 300 % d'ici 2050 !! Nous allons ici exposer en quoi la dette japonaise est soutenable.
La part de la dette publiques détenue par des nationaux en représente 90% [Source], de sorte que les intérêts sont versés très majoritairement à des nationaux.
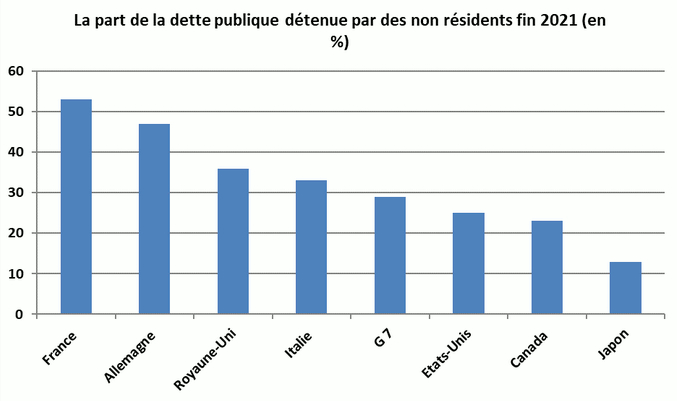
Source : fipeco.fr
La position extérieure du Japon est largement excédentaire. C'est même le numéro 1 mondial !
Cette performance de l'économie japonaise n'est pas étrangère à la qualité de l'enseignement et au niveau des fonds alloués à la R&D [source].
Le tableau suivant montre que le taux d'intérêt (10 ans) sur la dette publique japonaise est généralement inférieur à celui des autres États.
Belgique
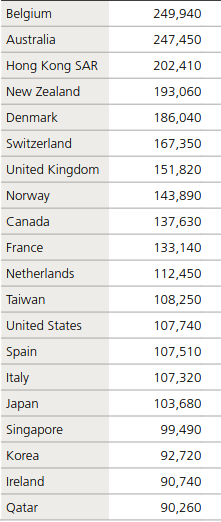
Suite à la crise pétrolière des années 1970 l'État belge a engagé de nombreux fonctionnaires dans le seul but de freiner la hausse du chômage. Il en a résulté une forte augmentation de la dette publique belge (mais aussi causée par le niveau élevé des taux d'intérêts en raison de l'inflation pétrolière). Cependant le niveau élevé de la dette publique belge (99 % du PIB en 2019) n'empêche pas l'économie belge d'être la plus riche au monde en terme de patrimoine médian par adulte (cf. tableau ci-dessous). La raison principale de cette situation est le taux très élevé d'épargne des ménages (environ 13% du revenu disponible). D'autres facteurs sont une politique redistributive généreuse qui nourrit la demande, ou encore la non taxation des plus-values. Mais rappelons, encore et toujours, qu'il s'agit là de simples corrélations, et que l'identification d'éventuelles relations de causalité, ainsi que leur sens, est beaucoup plus difficile à établir (ainsi la corrélation de deux variables peut être causée par un troisième variable, non identifiée).
Argentine
L'économie argentine a tout pour réussir : nombreuses richesses naturelles, main-d'œuvre qualifiée, agriculture orientée vers l'exportation, tissu industriel diversifié, faible dette publique (sauf lors de la crise de 2001-2002) [source]. Malgré cela, depuis la seconde guerre mondiale, le pays est confronté à de récurrentes périodes de forte inflation, et partant, à une instabilité de sa devise. Cette histoire économique de l'Argentine n'est sans doute pas étrangère à son histoire politique exacerbée par des basculements entre gouvernements très contrastés, soit vassalisés à Washington soit au contraire d'inspiration socialiste. Le basculement récurrent entre politiques économiques antagonistes n'a-t-il pas tendance à se traduire par de la surinflation ?
Dette interne
Dette externe
L'exemple de pays tels que le Japon et la Belgique montre qu'une dette publique élevée est d'autant plus supportable que la part d'investisseurs étrangers dans la dette nationale est faible. Autrement dit, une dette publique élevée est d'autant plus supportable qu'elle est financée par des agents économiques domestiques (ménages, entreprises, État).
En effet, en cas d'emprunt auprès de prêteurs étrangers dans leur devise il faut rembourser dans ces devises, ce qui nécessite ... d'en avoir (sauf si la monnaie nationale fait office de devise internationale, ce qui est le cas des USA). Pour ce faire il faut que la balance commerciale du pays emprunteur avec le pays prêteur soit suffisamment positive, c-à-d qu'il exporte suffisamment plus qu'il n'importe dans ses "échanges commerciaux" avec ce pays. Or ce n'est généralement pas le cas d'un pays emprunteur, de sorte qu'il ne lui reste comme solution que de faire ... de nouveaux emprunts pour rembourser les anciens. C'est typiquement ce qui se passe avec les prêts du FMI (en dollar ...), qui aboutissent à l'asservissement des pays emprunteurs.
Une alternative est d'échanger de la monnaie nationale contres des devises étrangères, mais il faut pour cela qu'il existe une demande étrangère pour la devise nationale. Plus la confiance dans celle-ci sera faible plus faible sera son cours.
Conclusion
"Magique"
infini ?
Nous avons vu qu'il n'existe pas de preuve scientifique quant à l'existence d'un niveau optimal absolu de la dette publique.
Comme le font remarquer Sterdyniak et Creel, tant que la dette apparaît désirée, qu’il est possible de l’émettre à de bas taux d’intérêt, qu’elle ne provoque ni tensions inflationnistes, ni déficit extérieur, il n’y a pas de preuve qu’elle est excessive [source].
Cela signifie-t-il que le niveau des dettes publiques pourrait croître indéfiniment, non seulement sans que cela pose problème mais qu'en outre ce soit même la clé du développement durable ? L'esprit humain appréhende difficilement la notion d'infini (*), ce qui explique qu'il est nous est difficile d'accepter cette thèse d'apparence magique. Ceci dit, il ne me paraît pas pour autant raisonnable d'en déduire qu'un endettement public infiniment croissant serait une politique de développement pertinente.
(*) Comment la notion d'infini est traitée en mathématique et informatique : democratiedirecte.net/intelligence#infini-informatique.
Mon avis peut se résumer en deux points :
- le niveau de la dette est moins important que sa dynamique (à un terme de plus de dix ans) ;
- cette dynamique (augmentation vs diminution) n'est pas une cause mais un symptôme indiquant si la politique de développement appliquée est pertinente (⇒ désendettement public) ou pas (⇒ endettement public).
Ainsi, fonder une politique de développement économique sur la réduction de la dette publique (ce que fait le traité de Maastricht, fondement de l'UE) est une absurdité, car elle consiste à supprimer le symptôme plutôt que la cause. La réduction de la dette publique doit être la conséquence d'une politique de développement efficace. Autrement dit, la réduction de la dette publique n'est pas un instrument mais un indicateur de politique de développement.
Bonne dette vs
Mauvaise dette
L'analyse de la dette publique, ainsi que la politique budgétaire, devraient donc moins se focaliser sur le quantitatif (le "combien" c-à-d le niveau de la dette) que sur le qualitatif (le "quoi" c-à-d les composantes de la dette). Il s'agit :
- d'identifier les éléments qui font croître ou baisser le solde budgétaire :
- dépenses justifiées insuffisantes vs dépenses injustifiées ;
- prélèvements obligatoires mal conçus et/ou mal administrés.
- d'identifier les mécanismes politiques et économiques par lesquels :
- des dépenses injustifiées sont engagées au détriment de dépenses justifiées ;
- des prélèvements obligatoires sont mal conçus et/ou mal administrés.
Dans une perspective plus fondamentale, l’endettement public peut se justifier :
- à court terme, comme mesure contracyclique pour compenser les effets négatifs des crises (notamment par des aides aux revenus des particuliers) ;
- à long terme, l’endettement public est justifié s’il permet d’accroître les actifs de l'État, et qu'ainsi la situation patrimoniale nette de l'État (actifs - passifs) s’accroisse (NB : il s'agit là d'une analyse seulement quantitative ; en termes qualitatifs, il importe que les actifs concernent une part suffisante de capacités de production, part actuellement très faible ...).
D'autre part, la politique monétaire est complémentaire à la politique budgétaire. Elle doit donc être confiée au gouvernement, et non à une Banque centrale indépendante (c-à-d privée).
Politique
monétaire
La Banque centrale devrait-elle financer systématiquement les déficits budgétaires en accordant à l'État des prêt inférieurs aux taux du marché (voire à taux nul) ? La réponse à cette question doit prendre en considération (notamment) les problématiques de l'inflation et du système politique.
Inflation. Lorsque la Banque centrale créé de la monnaie (par exemple pour "prêter" à l'État) il importe que cet argent serve à financer des investissements en capacité de production plutôt que de la consommation, sinon cette création monétaire peut se neutraliser via l'inflation (cf. /principes-monetaires].
Le prêt à intérêt nul diffère du don notamment en ce que le remboursement à la Banque centrale réduit la masse monétaire en circulation.
Lorsque l'État emprunte à des banques privées et que celles-ci prêtent en créant de la monnaie (cf. /creation-monetaire) le risque inflationniste est identique sauf qu'en plus l'État doit payer des intérêts. Si l'État emprunte à des agents non créateurs de monnaie, l'État transfère ainsi des ressources du secteur privé au secteur public, ce qui constitue un choix politique.
Dans le système politique actuel ("représentatif") le risque est élevé que le gouvernement abuse du financement monétaire des déficits budgétaires, et cela d'autant plus que le système politique n'est pas la démocratie directe, où – contrairement au système "représentatif" – les décideurs sont les payeurs.
Les gouvernements peuvent être tentés (et certains le font parfois, pendant une période limitée) de se financer par emprunt sans intérêt (ou à taux très faible) auprès de leur Banque centrale ("monétisation de la dette"). On notera cependant que suite à la crise de 2008 la très libérale Banque centrale européenne s'est montrée beaucoup plus généreuse avec les banques privées qu'avec les États ...
Recommandations. Dans l'attente d'un système politique véritablement démocratique la politique économique optimale pour la collectivité est selon nous la suivante :
- nationalisation de la Banque centrale ;
- les banques ne peuvent plus créer de la monnaie, ce qui implique que leur taux de réserves obligatoires est est dorénavant de 100% (autrement dit les banques ne peuvent plus prêter que de l'argent existant déjà) (cf. /creation-monetaire) ;
- la Banque centrale détient le monopole de la création monétaire, celle-ci est dorénavant réalisée à un taux de croissance relativement constant déterminé par la formule de la théorie relative de la monnaie (soit 5,5% par an dans des pays tels que la France ou la Belgique), et distribuée également et gratuitement entre les personnes physiques (/financement-distributif).
Démocratie
Les faits évoqués dans le présent article suggèrent qu'un accroissement rapide des dettes publiques peut être autant le fruit de gouvernements "populistes" que le signe d'une grave régression démocratique.
Si le secteur public est contrôlé par une oligarchie, celle-ci privilégie son intérêt privé au détriment de la collectivité. La corruption de décideurs politiques a pour effet (i) que les ressources publiques sont insuffisantes en raison de privilèges fiscaux accordés aux plus riches, et (ii) que les ressources disponibles sont allouées à des dépenses injustifiées (dépenses de prestige, investissements inadéquats, intérêts de la dette, ...) privilégiant les (actionnaires de) puissants lobbies économiques (banques, armement, pharmacie, ...) au détriment de la collectivité.
À cela il faut ajouter que :
les décideurs politiques sont incités à provoquer la faillite de services publics rentables afin de justifier leur privatisation au bénéfice de grandes entreprises privées qui "sponsorisent" ces mêmes décideurs ;
le projet d'Union européenne ayant pour ambition finale de se substituer aux nations qui la composent, la classe politique européiste peut voir la "faillite" des États européens comme un moyen de forcer leur substitution par l'Union européenne.