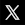XIII.6. Thermodynamique
Introduction
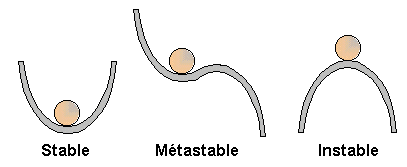
Pourquoi parler physique dans une publication consacrée au travail ? En fait la question qu'il faudrait poser est plutôt : comment se fait-il que la théorie économique classique enseignée dans nos universités ne fait aucune référence aux lois physiques qui régissent les relations énergétiques entre corps inertes comme vivants ? Pour faire de l'économie une véritable science, plutôt qu'une idéologie et une propagande de classe dirigeante, le shéma ci-contre constitue un bon point de départ. Il nous fait réaliser toute la supercherie de la dialectique extrayant de la matière un supposé second facteur (agent) de production, appelé "capital", alors qu'il ne s'agit bien évidemment que d'un moyen (objet) de production.
Si l'économie ne peut être science que si elle est exacte, il demeure que cette science n'est "économique" que parce qu'elle est humaine et sociétale. Pour approfondir ce point, lire l'article "Travail et valeur".
Force et travail
Force = Masse * Accélération
(unité : kg m s-2, appelée le newton)
- Exercer une force c'est accélérer le déplacement d'une masse. On peut voir aussi la masse comme une coefficient de proportionnalité entre la force et l'accélération.
- Les forces sont donc liées aux accélérations et non aux vitesses. Cela est lié au principe d'inertie dont il découle qu'il n'est pas besoin de subir une force pour être en mouvement.
Travail = Force * Déplacement
Travail = Masse * Accélérat. * Déplacem.
(unité : kg m2 s-2, appelée le joule)
- Réaliser un travail, c-à-d "dépenser" (nous verrons qu'il s'agit en fait de transformer) de l'énergie, c'est exercer une force sur une certaine distance. On peut dire aussi qu'une force exercée sur une certaine distance se transforme en travail.
-
Dans le cas des gaz on a :
Force = Pression * Surface
substitué dans n_W=F*L ⇒
Travail = Pression * Surface * Déplacement = Pression * ΔVolume
Exemple : travail d'un piston comprimant un gaz
Puissance = Travail / Temps
Approfondissons les notions de force et de travail.
Force =
Masse *
Accélér.
Galilée, qui avait déjà constaté au 16° siècle que les comètes avaient tendance à suivre une trajectoire retiligne selon un mouvement uniforme, a énoncé le principe d'inertie qui stipule que tout objet placé dans un référentiel inertiel et soumis à des forces nulles ou qui se compensent est soit immobile, soit en mouvement rectiligne uniforme.
On entend par force « toute cause capable de modifier l'état de repos ou de mouvement d'un corps », c-à-d qui explique qu'un corps immobile se met en mouvement, ou qu'un corps en mouvement rectiligne à vitesse constante change de vitesse, direction ou sens. L'intérêt pratique du concept de force apparaît pleinement dans sa représentation par un vecteur composé d'un point d'application, d'une direction, d'un sens et d'une intensité. Cette modélisation mathématique constitue le fondement de la physique dynamique et a facilité l'invention de machines mécaniques (PS : l'histoire des sciences et techniques suggère cependant que la relation entre théorie et développement serait biunivoque). Il existe divers type de forces, que l'on peut classer en deux groupes :
- forces de contact : frottement, pression, liaison ;
- forces à distance : gravitationnelle, électrostatique, électromagnétique [approfondir].
Chacune de ces force est définie par sa propre formule, mais toutes ont en commun (puisque toutes sont des forces) que leur valeur est égale à M * A. Le cadre suivant illustre le cas de la force de gravitation.
Force gravitationnelle
Deux corps de masse M1 et M2 et séparés d'une distance D (entre leurs centres de masse) subissent une force d'attraction (dite gravitationnelle) = g * M1 * M2 / D2 où g est la constante gravitationnelle, dont on a évalué expérimentalement la valeur à 6,6742×10-11. Dès lors l'accélération que subit un corps de masse M à la surface d'une planète de masse Mp sur laquelle il repose s'obtient par approximation en posant D = Rayon de la planète --> g * M * Mp / R2 = M * A --> A = g * Mp / R2 ... qui montre que A, l'accélération gravitationnelle, est indépendante de la masse du corps qui la subit, et fonction des masse et volume de la planète qui l'exerce. Ainsi on peut calculer que A vaut 9,8 m/s2 sur la Terre et 1,6 m/2 sur la Lune. PS : la force gravitationnelle est également appelée "force de pesanteur" ou encore "force de chute libre".
N.B. L'équation gravitationnelle (découverte par Isaac Newton) implique donc qu'un corps peut exercer une action sur un autre à distance.
La masse est la mesure de l'inertie de translation d'un corps. L'inertie d'un corps est sa tendance à conserver son mouvement. Autrement dit, la masse d'un corps est sa résistance à toute modification de son mouvement (que ce soit en direction, sens ou vitesse).
Poids = Masse * Ag Ne pas confondre "poids" et "masse" : le poids est la force de pesanteur, soit le produit de la masse par l'accélération gravitationnelle (aussi appelée "accélération de pesanteur").
Un corps est dit « à l'équilibre » si son accélération est nulle, c-à-d lorsqu'il est soit au repos soit en mouvement à vitesse constante.
Nous verrons plus loin qu'un système est dit "à l'équilibre thermodynamique" lorsque l'énergie qu'il contient y est uniformément répartie.
L'égalité F = M * A (dite deuxième loi de Newton ou loi fondamentale de la dynamique) stipule donc que si la résultante des forces appliquées à un corps est non nulle, alors ce corps subit une accélération, laquelle est proportionnelle au rapport entre la force résultante et la masse du corps : A = F / M.
Travail =
Force *
Déplacem.
Une force travaille (ou effectue un travail) lorsque son point d'application se déplace. Le travail est la relation entre deux corps par laquelle une quantité d'énergie équivalente est transformée et transférée lors du déplacement du point d'application (travail et énergie sont tous deux exprimés en joules : kilogramme * mètre2 / seconde2 ) [approfondir].
Il y a donc un rapport de proportionnalité entre le travail (mécanique) fourni par l'ouvrier et l'énergie qu'il a préalablement assimilée (nourriture). Le travail se transforme en énergie : quand on exerce une force on dépense de l'énergie. La "consommation" d'énergie est en réalité transfert et transformation d'énergie entre l'ouvrier et le corps sur lequel il exerce son travail (ou entre une objet en mouvement sur ce corps : c'est l'énergie cinétique).
Qu'en est-il du travail intellectuel ? La physique peut-elle décrire ce phénomène ? Nous y reviendrons lorsque nous aborderons la physique quantique.
Énergie
2. Principes
3. Modélisation
4. Exemples
5. Relativité
Définition
Énergie = Masse * (Vitesse de la lumière)2 (unité : kg m2 s-2, appelée le joule)
N.B. Cette égalité concerne tous les corps de masse non nulle (et ne s'applique donc pas aux photons, pour lesquels E=p*c où p est l'impulsion, encore appelé momentum), et (/même ?) au repos. Elle établit donc l'équivalence entre masse et énergie.
- Selon la théorie de la relativité restreinte (Einstein), les corps de masse non nulle ne peuvent atteindre la vitesse maximale universelle (c ≈ 18 millions km/h dans le vide). La masse des photons étant nulle (dans l'état actuel de la technologie ...), on en déduit que c est également la vitesse de la lumière.
- On notera que travail et énergie ont la même unité de mesure. Nous verrons plus loin que travail mécanique et chaleur sont deux formes particulière d'énergie.
Enfin la puissance se mesure en joule/s (appelée le watt), et est donc un débit d'énergie. Ainsi une ampoule de 10 watts dissipe chaque seconde 10 joules d'énergie (PS : nous verrons que le verbe "dissiper" est ici fondamental).
Tout corps (inerte ou vivant) doit, pour être en mesure de fournir du travail, contenir une énergie potentielle (exemples : un corps placé à une certaine hauteur, un corps élastique écarté de sa position d'équilibre, l'énergie cinétique d'une comète, ...).
Un corps en mouvement rectiligne possède une énergie cinétique (ou de translation), que l'on défini et mesure par la formule : Ec = M * V2 / 2 [approfondir].
Principes
Nous allons énoncer ici les trois principes fondamentaux de la thermodynamique :
- premier principe : l'énergie se conserve quantitativement (on ne peut ni la créer ni la détruire) ;
Peut-on considérer le théorème de Noether comme une démonstration du premier principe ? : des réponses ...
second principe : l'énergie peut être transformée d'une forme en une autre (chimique, thermique, mécanique, électrique, ...), mais la transformation sera nécessairement accompagnée d'une dégradation qualitative (phénomène de dissipation), ce qui rend toute transformation irréversible (une transformation "inversée" ne l'est qu'en apparence) ;
Les ingénieurs formulent plutôt le second principe comme suit : « il est impossible de convertir de la chaleur en travail à partir d'une seule source de chaleur : la chaleur ne peut donner lieu à un flux que du plus chaud vers le plus froid ». Nous verrons plus loin, dans la section #machine-carnot, les fondements de cette version. Quant aux physiciens, ils préféreront sans doute exprimer le second principe en fonction de l'entropie : « l'entropie d'un système isolé demeure constante tant qu'il subit des transformations réversibles, et augmente dès qu'une transformation est irréversible » [source p. 38-39].
- troisième principe :
- version minimaliste (prouvée) : la dissipation d'énergie (appelée entropie) subie par un cristal parfait à 0 kelvin est nulle ⇔ l'entropie d'un système se rapproche d'une valeur constante lorsque sa température se rapproche du zéro absolu ;
- version augmentée (non encore démontrée) : l'énergie tend à maximiser sa vitesse de dissipation (loi de production maximale d'entropie).
Une théorie affirme que pour ce faire les systèmes ouverts s'auto-organisent, en mémorisant de l'information sur leur environnement, et que ce faisant elles maximisent le flux d'énergie qui les traversent. Nous approfondirons ces notions dans la section consacrée aux structures dissipatives.
Ainsi dans les sections suivantes nous allons voir que tout système (organisme vivant, machine, cyclone, ...) :
- est caractérisé par un rendement (R), dont une mesure est la différence entre énergie totale engagée (E) et la part de celle-ci qui a été dissipée en chaleur non utilisable (C), le tout divisé par le travail fourni (W) : R = ( E - C ) / W.
N.B. Par chaleur "dissipée" on entend le fait qu'elle n'est pas utilisée, voire pas utilisable. L'expression « énergie dissipée en chaleur non utilisable » est donc un pléonasme.
- le principe de conservation (aucune matière ni énergie n'est créée ou détruite, mais seulement transformée) se formule par E = W pour ce qui concerne l'énergie mécanique (énergie mécanique = travail).
- le principe d'entropie (la transformation de la matière/énergie est accompagnée d'une dégradation qualitative sous forme de chaleur dissipée) se formule par C > 0.
Ces principes physiques valent également pour les système biologiques : ne serait-ce qu'avec l'écoulement du temps (vieillissement), tout système passe d'une forme organisée à une forme désorganisée. Nous verrons dans la suite de ce document que la variation d'entropie (ΔC) est une mesure de la dissipation, et que :
- l'augmentation d'entropie (ΔC > 0 : désorganisation) est propre aux systèmes fermés (ce qui est le cas de l'univers considéré comme "le tout ultime") ;
- la diminution d'entropie (ΔC < 0 : organisation) serait propre aux systèmes ouverts, qui en étant ainsi traversés par des flux d'énergie, font apparaître des structures organisées.
Mais ne brûlons pas les étapes. Il nous faut d'abord approfondir la notion d'énergie.
Modélisation
L'énergie ne peut-être créée mais seulement transformée d'une forme en une autre. Sur base de ce postulat on peut alors décrire comme suit l'évolution énergétique d'un corps en chute libre entre le moment de son lâché et celui de l'impact :
- avant le lâché (soit à t0) :
- son énergie potentielle (ici, de pesanteur) vaut l'énergie consommée/transférée/transformée par le travail nécessaire pour amener le corps de masse M à une hauteur D : Ep(t0) = M * A * D (où A est ici l'accélération gravitationnelle;
- son énergie cinétique est nulle : Ec(t0) = 0 ;
- entre le moment du lâché et celui de l'impact (ti ), l'énergie potentielle va passer de M * A * D à zéro, tandis que l'énergie cinétique va passer de zéro à un maximum tel que :
Ec(ti) = Ep(t0) ⇔ M * V 2 / 2 = M * A * D
... ce qui permet de calculer la vitesse du corps au moment de l'impact : V(ti) = (2 * A * D) 1/2 (NB : elle est indépendante de la masse du corps mais fonction de D : dans une chambre à vide où il n'existe aucune force de frottement un plume tombe aussi vite qu'une enclume).
L'énergie potentielle s'est donc transformée en énergie cinétique pendant ce mouvement de chute libre. Mais à tout instant la somme de l'énergie potentielle de pesanteur et de l'énergie cinétique est constante.
Isaac Newton a ainsi montré que c’est la masse qui fait accélérer un objet lorsqu’il est placé dans un champ de gravité ; qui le fait “peser” lorsqu’il ne peut bouger ou qui oblige à utiliser une force pour le mettre en mouvement. Une force d’autant plus intense que ladite masse est importante.
Dans cet exemple de chute libre on a fait abstraction des forces de frottement, mais cela n'altère pas la validité du raisonnement car tous les types de force et tous les systèmes composés de forces (même de types différents) sont soumis à cette « loi de conservation de l'énergie » (premier principe de la thermodynamique), qui stipule que l'énergie :
- peut-être échangée entre deux corps/systèmes ;
- peut être transformée d'une forme en une autre (ex. : d'énergie cinétique en énergie mécanique) ;
- mais qu'elle ne peut être ni créée ni détruite.
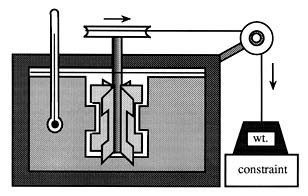
Exercice : amusez-vous à imaginer ce que ce croquis raconte. Quelques indices : (i) en faisant varier la hauteur du bloc "constraint" on fait varier la hauteur de la chute de la masse "wt" ; (ii) le rectangle noire délimite un système isolé thermiquement, et rempli d'eau ...
Différence de potentiel. La notion d'énergie potentielle induit celle de différence de potentielle, qui est à la base du processus dynamique (courant, débit, ...). D’une façon générale on dit que les courants d’énergie s’écoulent des régions de haut potentiel vers les régions de bas potentiel, comme l’eau s’écoule nécessairement des sommets vers la plaine [approfondir], ou la chaleur d'une source chaude vers une source froide.
- Bien sûr il est possible de faire remonter de l'eau (cf. pompe) ou de transférer de la chaleur d'une source froide vers une source chaude (cf. frigo). Mais – nous dit le premier principe – cela est impossible sans apport d'énergie supplémentaire au système considéré.
- Dans le phénomène électrique les différences de potentiel se mesurent en volts et les débits en ampères. Un courant de 1 ampère fourni par une différence de potentiel de 1 volt fournit une énergie de 1 joule par seconde, c’est-à-dire une puissance de 1 watt.
Énergie en psychologie
D'un point de vue psychologique on pourrait voir le désir comme une (la ?) source d'énergie de la psyché :
- le désir de réalisation (personnelle, d'un projet, ... ) est connoté positivement ;
- le désir de domination (ou de soumission) est généralement connoté négativement, sauf dans certains milieux (fascisme, sado-masochisme) ou contexte (certains tests de sélection de cadres supérieurs) ;
- le désir sexuel est souvent connoté négativement (par exemple dans certains milieux puritains) ;
- ...
Ou faut-il voir le désir plutôt comme une force ?
Mais ces analogies entre physique et psychologie sont-elles pertinentes ?
Exemples
Voici quelques illustrations des premier (conservation) et second (transformation & dégradation) principes de la thermodynamique [source] :
- Naturelles :
- Une comète qui se rapproche du soleil voit sa vitesse, donc son énergie cinétique, augmenter alors qu’elle perd de l’énergie potentielle. Après avoir contourné le soleil, l’énergie cinétique qu’elle a ainsi acquise se transforme de nouveau intégralement en énergie potentielle lorsqu’elle repart au loin tout en perdant de la vitesse. Lorsqu'une comète percute une planète son énergie potentielle (en occurrence cinétique) est transformée d'une part en énergie mécanique (provoquant le cratère), et d'autre part en chaleur.
- Le feu, réaction chimique vive d’oxydation par l’oxygène de l’air, convertit de l’énergie chimique en chaleur.
Le rayonnement électromagnétique (par exemple la lumière du soleil) produit – lorsqu’il est absorbé – un échauffement (par exemple d'un morceau de métal exposé au soleil), et propage donc de l’énergie.
- "Artificielles" :
- Une partie de l'énergie que vous "consommez" (en fait transformez) en remontant le ressort (ou le poids) de votre vieille horloge mécanique sera dégradée sous forme de chaleur (qui provoque votre transpiration), le reste étant stocké dans le ressort du mécanisme (énergie potentielle du ressort). Une foi que vous déclenchez le mécanisme de l'horloge, cette énergie potentielle mécanique est transformée en énergie cinétique (mouvement du balancier). Cependant, en raison des forces de frottement ce mouvement ne sera pas perpétuel (contrairement à celui de la comète qui dans le vide spatial n'est soumise à aucune force de frottement) : le balancier de l'horloge va nécessairement s'arrêter après un certain temps, lorsque toute l’énergie potentielle du ressort aura été transformée en chaleur. Il y a ici irréversibilité en ce sens que l'on ne peut pas remettre en marche le balancier en chauffant l’horloge.
- Une pile transforme directement de l'énergie chimique en énergie électrique.
Relativité
Les forces d'interaction que nous venons de passer en revue concernent les phénomènes physiques "de dimension humaine" (physique "newtonnienne"), mais ne permettent pas d'expliquer de façon satisfaisante les phénomènes :
- à vitesses proches de la vitesse de la lumière (--> recourt à la relativité, qui fonde les interactions sur la courbure de l'espace-temps par la matière) [approfondir] ;
- dont le champs de gravitation est à intensité et variabilité élevée de sorte qu'il influence la géométrie de l'espace (--> recourt également à la relativité) ;
- microscopiques tels que la couleur ou la dureté d'un corps (--> recourt à la mécanique quantique, qui fonde les interactions sur des échanges entre particules élémentaires sous la forme de photons, bosons et gluons).
Relativité
galiléenne
Historiquement il y d'abord eu la relativité galiléenne (17e siècle), qui stipule que (dans un mouvement rectiligne et uniforme) l'espace et le temps sont absolus c-à-d que les distances, durées et accélérations sont invariantes entre référentiels différents. Par contre la vitesse est relative au référentiel choisi pour effectuer la mesure (vous avez déjà expérimenté cela lorsque vous êtes dans un train en gare à côté d'un autre et que l'un démarre, mais que vous ne savez pas lequel) [approfondir].
Relativité
restreinte
Mais lorsqu'au 19e siècle il est apparu que la vitesse de la lumière (vitesse maximale) était invariante quel que soit le référentiel, la transformation de Galilée (formule pour traduire les mesures entres différents référentiels) a du être remplacée par la transformation de Lorentz (dont elle est un cas particulier, celui de vitesses faibles). Or la transformation/formule de Lorentz implique qu'à des vitesses élevées (du même ordre de grandeur que celle de la lumière), espace et temps deviennent aussi relatifs au référentiel [source].
Concrètement :
- l'espace à trois dimensions spatiales se voit ajouter une quatrième dimension : le temps ;
- il existe une vitesse maximale, qui est celle de la lumière.
Énergie et matière. Une loi fondamentale de la théorie de la relativité énonce une relation entre matière et énergie : tout corps contient/représente une quantité d'énergie égale au produit de sa masse et du carré de la vitesse de la lumière dans le vide : E = M * C2 où C a une valeur constante qui est la limite maximale à la vitesse de tout corps en mouvement (PS : la vitesse est maximale dans le vide, en raison de l'absence de frottements).
Énergie nucléaire. Cette égalité découverte par Einstein - et médiatisée comme aucune autre - montre que les sources d'énergie ne manqueront jamais puisque tout dans l'univers - matière et rayonnement - est énergie. En outre, du fait de l'énormité du facteur C2, une perte de masse infime à l'échelle humaine peut dégager une énorme quantité d'énergie (PS : la libération d'énergie requiert une réduction de masse en vertu du principe de conservation de l'énergie). Au niveau technologique le phénomène est exploité au moyen de réactions nucléaires déclenchées soit par fission soit par fusion d'un noyau d'atome (PS : la fusion libère trois à quatre fois plus d'énergie que la fission).
- Puissance de la fission. Un gramme de matière que l'on annihilerait par collision avec de l'antimatière correspond à environ 1014 joules, soit approximativement l'énergie dégagée par la première bombe nucléaire qui en 1945 détruisit Hiroshima ... et sa population civile [source : E=mc2 sur Wikipedia].
- Fusion contrôlée. La libération d'énergie par la fusion nucléaire est maîtrisée depuis 1952 (bombe H). On est donc aujourd'hui capable de déclencher une fusion nucléaire, mais pas encore de contrôler la réaction, ce qui permettrait d'utiliser la fusion comme source d'énergie pour construire plutôt que pour détruire. Le projet ITER est actuellement le plus avancé en matière de R&D sur la fusion nucléaire contrôlée, mais on n'est pas encore capable de libérer plus d'énergie sous contrôle qu'on en "consomme" pour ce faire ...
Relativité
générale
Le "mouvement élémentaire" du référentiel inertiel, la translation rectiligne uniforme, est ici remplacée ou plutôt élargie à celle de chute libre dans un champs gravitationnel. Celui-ci a pour effet de courber l'espace-temps.
Alors que la relativité générale traite de l'infiniment grand, la mécanique quantique traite de l'infiniment petit, de sorte que l'on s'approche d'une "théorie du tout".
Mais revenons à la relativité restreinte. Certaines énergies seraient donc plus efficacement transformables en énergie mécanique que d'autres, d'où la notion de rendement d'une transformation, que nous allons maintenant développer en approfondissant le second principe de la thermodynamique.
Entropie
2. Machine de Carnot
3. Énergie interne
4. Irréversibilité
5. Entropie et économie
Dissipation
Revenons sur les notions de transformation et de dégradation de l'énergie, présentées dans la section précédente.
Premier principe. L'énergie ne peut être ni créée ni détruite mais seulement transformée d'une forme en une autre (premier principe de la thermodynamique, encore appelé principe de conservation).
Second principe. Cependant cette transformation est généralement accompagnée d'un phénomène de dissipation par lequel du travail mécanique est transformé en chaleur (énergie calorifique), sous l'effet de forces de frottement, ce qui rend toute transformation irréversible (second principe de la thermodynamique, encore appelé principe d'irréversibilité). La chaleur est un forme dégradée d'énergie car la transformation inverse – de chaleur en énergie mécanique – est toujours partielle, de sorte que toute transformation est irréversible (on peut cependant concevoir des systèmes dont la transformation est d'apparence réversible, si les différences entre le système avant transformation et après transformation+réversion sont relativement négligeables).
Conclusion. L'énergie (et partant la matière, étant donné la relation E=Mc2) se conserve donc, mais se dégrade aussi irrémédiablement. C'est le phénomène du vieillissement (les montagnes et les étoiles aussi naissent et meurent). Il est aussi le fondement thermodynamique du cycle de la vie biologique.
"Consommer" de l'énergie signifie donc en réalité "dégrader" de l'énergie. D'autre part l'expression "retourner à la poussière" pour décrire la mort prend ici toute sa signification.
Machine de Carnot
On ne peut convertir qu’une partie seulement de la chaleur en travail (énergie mécanique). Comment s'en est-on rendu compte ? Commençons par constater qu' il est plus difficile de transformer de la chaleur en travail que l'inverse : ainsi il suffit de frotter du bois sec contre du bois sec pour produire de la chaleur, mais il ne suffit pas de chauffer du bois pour le mettre en mouvement. Si l’énergie mécanique peut être intégralement convertie en chaleur, la réciproque n’est pas vraie.
Lorsqu'au 18° siècle on a tenté de faire fonctionner les premières machines à vapeur on s'est rendu compte que pour transformer de la chaleur en énergie mécanique il faut utiliser des transformations réversibles, en l'occurrence des cycles de transformation "pression <--> travail". Mais pour fonctionner ces cycles requièrent d'extraire de la chaleur d’une source chaude (pour produire de la vapeur) et d'en rendre une partie à une source froide (pour la condenser).
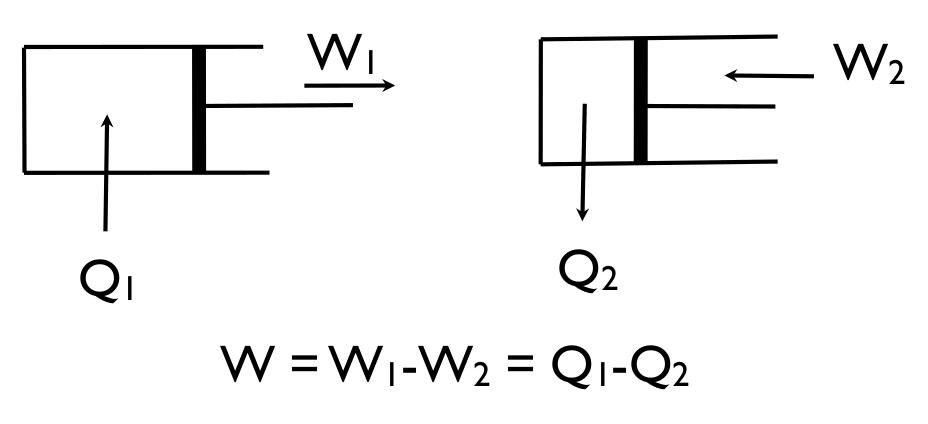
Soit Q1 la chaleur fournie par la source chaude. À lʼaller la vapeur pousse le piston qui fourni un travail W1, mais pour ramener le piston au point de départ, il faut refroidir le cylindre en cédant une partie Q2 de la chaleur à une source froide et fournir un travail W2. Il y a donc nécessité de mettre en réserve l'énergie nécessaire pour pouvoir repousser le piston [source]. Il en résulte que le mouvement perpétuel est physiquement impossible.
- La chaleur se propage toujours d'un corps chaud vers un corps froid, et jamais l'inverse (sauf, pour ce faire, à fournir du travail, comme dans un frigo).
- Régulation. Si trop d'énergie est emmagasinée pour repousser le piston le moteur s'emballe. Si pas assez, il cale. Ainsi tout moteur thermique est fondamentalement instable, et doit par conséquent être régulé. C'est pourquoi James Watt a dû équiper sa machine à vapeur d’un régulateur à boule.
On ne peut donc convertir qu’une partie seulement de la chaleur en travail. Cette partie est proportionnelle au différentiel de température entre les deux sources. Cependant, les températures des deux sources tendant à s’uniformiser, l’énergie thermique devient définitivement inutilisable, sauf à rétablir une différence de température entre les deux sources, ce qui requiert de fournir du travail [source].
Ainsi Roddier énonce le second principe de la thermodynamique de la façon la plus élaborée : « On ne peut durablement produire du travail mécanique que par des cycles fermés de transformations extrayant de la chaleur d’une source chaude pour en rendre une partie à une source froide ».
Efficacité
énergétique
d'une machine
Ces principes sont modélisés dans le cycle théorique de Carnot (théorique car il fait abstraction des forces de frottement). Ce modèle montre que l'efficacité énergétique (mesurée par le rapport énergie utile en sortie / énergie fournie en entrée) d'une machine thermique est égal à 1 - Tf / Tc (où Tf et Tc sont respectivement les températures des sources froide et chaude, exprimées en kelvin. Cette efficacité est donc nécessairement inférieure à 100% car pour être égal à 1 il faudrait que Tf = 0. Or le zéro de l'échelle kelvin est le zéro absolu, qui correspond à l'absence d'agitation thermique, laquelle est pratiquement impossible en raison des propriétés quantiques des particules.
Application. « Si la vapeur d’eau était commode à utiliser, à cause des larges variations de volume qu’elle procure, elle limitait les différences de température à moins de 100° et, par là, limitait considérablement le rendement de la machine. Utiliser un fluide au voisinage de son point critique serait encore pire, car le rendement de la machine tendrait vers zéro » [source].
Un cycle réversible est tel que Q1 / T1 = Q2 / T2 c-à-d que le rapport Q/T se conserve. NB : la réversibilité est nécessairement limitée dans le temps et l'espace puisque fondamentalement toute transformation est irréversible. C'est Rudolf Clausius (1822-1888) qui, se basant sur les travaux de Sadi Carnot (1796-1832), appela ce rapport "entropie" [source p.41].
Vitesse. Roddier précise que « une transformation est d’autant plus proche de la réversibilité qu’elle est effectuée lentement » [source p. 165].
Ainsi l'entropie (S) est telle que :
dS = Q / T (unité : calories / degrés Kelvin)
On peut aussi formuler n_dS=Q/T par ΔS = ∫ 1 / T dQ. Le lecteur est vivement invité à revoir si nécessaire la différence entre les notations Δ, d, ∂ et δ : wikipedia.org/Notations_delta_en_sciences.
Une machine thermique idéale dont toutes les opérations seraient réversibles est appelée "machine de Carnot" [source p. 171]. Sont efficacité énergétique est l'efficacité maximale qu'une machine puisse approcher.
La planète Terre, une machine thermique
Roddier note que la biosphère fonctionne comme une machine thermique. Elle reçoit de la chaleur du soleil, la source chaude (à température proche de 6.000°K). Le ciel nocturne quant à lui est la source froide (à température absolue proche de 3°K. La biosphère peut ainsi produire du travail mécanique avec un rendement atteignant presque 100% grâce à l'intermédiaire des cycles de réaction chimique. On peut ainsi considérer l'écosystème comme un moteur à deux temps. Dans un premier temps, les plantes captent l’énergie solaire et l’emmagasinent sous forme de carbone chimiquement réduit. Dans un second temps, l’oxydation du carbone dégage la chaleur émise sous forme de rayonnement infrarouge en direction du ciel nocturne [source p. 171].
Roddier souligne également l'analogie entre le cycle de Carnot ou encore du cycle convectif, avec le cycle des saisons [source p. 89] :
| Carnot | Convectif | Saison |
|---|---|---|
| Expansion isotherme | Réchauffement | Hiver (germination) |
| Expansion isentropique | Ascension (extension) | Printemps (croissance) |
| Compression isotherme | Refroidissement | Été (apogée) |
| Compression isentropique | Descente (compression) | Automne (régression) |
NB : passée l'équinoxe d'hiver, la terre se réchauffe lentement.
Le fait que la chaleur ne peut être intégralement transformée en travail mécanique induit la notion d'énergie libre d'un système fermé, à savoir l'énergie utilisable qu'il contient, c-à-d la quantité totale d'énergie qu'il contient (énergie interne) moins celle qu'il dissipe sous forme de chaleur. Pour qu'un système fermé conserve sa quantité d'énergie libre il faudrait donc que les transformations d'énergie liées à son fonctionnement soient toutes réversibles (ce qui n'existe pas dans la réalité).
- Les ingénieurs utilisent plutôt la notion d'exergie, très similaire à celle d'énergie libre.
- L'énergie interne d'un système fermé « c-à-d isolé mécaniquement et thermiquement du milieu extérieur » est constante. Nous verrons plus loin que dans un système isolé l'énergie mécanique se dissipe peu à peu en chaleur de sorte que tout mouvement cesse. Les différences de température s'estompent de sorte qu'il n'est plus plus possible de produire de l'énergie mécanique.
Énergie interne
On appelle "énergie interne" (U) la quantité totale d'énergie que contient un système.
Le premier principe de la thermodynamique implique que :
dU = W + Q où
- W est le travail mécanique reçu par le système ;
- Q est la chaleur reçue par le système.
En substituant W = -P * dV n_W=-P*ΔV et dS = Q / T n_dS=Q/T dans n_dU=W+Q on obtient que :
dU = -P * dV + T * dS
Un système est dit "isolé" s'il ne peut pas échanger (recevoir ou fournir) du travail mécanique ou de la chaleur avec le milieu extérieur. Dans ce cas :le premier principe de la thermodynamique implique que dU = 0
le second principe de la thermodynamique implique que dS ≥ 0 : soit l'entropie reste constante (tant que le système subit des transformations réversibles), soit elle augmente (dès qu'il subit des transformations irréversibles). Lorsque l'entropie atteint sa valeur maximale, toute évolution cesse. On dit que le système a atteint l'équilibre thermodynamique [source p. 40].
Irréversibilité
Irréversibilité. La température est la mesure de la chaleur (expression du mouvement microscopique des molécules) observée au niveau macroscopique. En raison de la nature désordonnée/aléatoire caractérisant le mouvement des molécules, la mesure de la température d'un gaz ne peut être qu'une mesure probabiliste du mouvement de ses molécules (énergie cinétique moyenne des molécules), c-à-d des positions et vitesses probables d'une énorme quantité de molécules formant un système mécanique complexe [source]. La (ir)réversibilité est donc est liée à notre (in)capacité de contrôle du mouvement des molécules c-à-d in fine à notre (mé)connaissance de leur position et vitesse respectives dans le système observé.
Macro/micro. Initialement associée à un mouvement macroscopique, commun à tout un ensemble de molécules, l'énergie mécanique se transforme en chaleur lorsque ce mouvement se disperse pour devenir un mouvement désordonné, différent pour chacune des molécules du système. Il convient cependant de distinguer l’état microscopique d'un corps/système (défini par la position et la vitesse de chacune de ces molécules) de son état macroscopique (défini par des grandeurs moyennes telles que sa pression et sa température). Le physicien Roger Balian explique que « le principe de conservation de l'énergie résulte de la conservation à l'échelle microscopique de l'énergie mécanique. (...) Le passage d'une échelle à l'autre entraîne une modification qualitative des concepts et des propriétés. La microphysique est discontinue, probabiliste, linéaire, réversible, alors que la physique macroscopique qui en découle est continue, déterministe, non linéaire, irréversible ».
États macro et microscopiques
| Macroscopique | Microscopique | |
|---|---|---|
| Énergie | travail mécanique | chaleur |
| Entropie | faible | élevée |
| Information | connue | inconnue |
On appelle "entropie" la mesure de la dégradation énergétique. Au niveau microscopique l'entropie est également une mesure du désordre puisque le phénomène calorifique est caractérisé par le mouvement désordonné/aléatoire des particules. Autrement dit, l’irréversibilité thermodynamique provient du passage de l’ordre au désordre, et cette dégradation correspond à une perte d'information sur la trajectoire particulière de chacune des particules. L'entropie est donc une mesure de notre perte/manque d'information concernant l'état microscopique d'un système observé.
L'irréversibilité peut donc être définie comme suit : « une transformation est irréversible si, et seulement si, il y a perte d'information sur le système » [source].
Quant à l'entropie elle est telle que :
- dans un système isolé, c’est-à-dire qui ne peut échanger de l'énergie avec l'extérieur (en perdre ou en gagner), l'entropie ne peut qu'augmenter (⇔ il existe des transformations irréversibles) ou rester constante (⇔ transformations toutes réversibles ⇔ le système reçoit autant d'entropie qu'il en fournit) ;
- l'entropie de peut diminuer que dans des systèmes vérifiant trois conditions :
- ils sont limités dans l'espace et le temps ;
- ils reçoivent du travail (et donc de l'énergie) provenant de l'extérieur ;
- leur fonctionnement (transformation d'énergie) est lié à une augmentation accrue d'entropie à l'extérieur.
Exemple. Si vous mettez des glaçons et de l’eau chaude dans une bouteille Thermos, vous obtenez de l’eau froide. C’est une transformation irréversible durant laquelle l’entropie augmente. Si vous y mettez de l’eau froide vous ne verrez jamais apparaître des glaçons et de l’eau chaude. L’entropie ne pourra pas diminuer. Par contre, si vous mettez de l’eau froide dans votre réfrigérateur et que vous le branchez sur une prise électrique, vous verrez apparaître des glaçons à l’intérieur et un dégagement de chaleur à l’extérieur. L’entropie a diminué provisoirement et localement grâce à un apport extérieur d’énergie électrique. Ce n’est que provisoire car la chaleur produite derrière votre réfrigérateur va se dissiper dans l’atmosphère et vos glaçons vont fondre dans votre boisson, achevant de dissiper toute l’énergie électrique que vous avez consommée. Au total, l’entropie aura définitivement augmenté [source].
Les organismes vivants étant par nature des systèmes organisés (NB : organisation, organisme, organes ...) sont donc nécessairement des systèmes (i) ouverts ; (ii) recevant de l'énergie en provenance du reste de l'univers ; (iii) transformant cette énergie, ce qui implique une augmentation d'entropie dans le reste de l'univers.
Entropie et économie
L'économiste quant à lui est amené à distinguer énergie primaire et énergie finale, la seconde étant nécessairement inférieure à la première en raison des pertes de conversion des énergies primaires en énergies finales.
Découplage
Les premier et second principes de la thermodynamique imposent ainsi une limite physique au principe de découplage cher aux partisans de la transition énergétique vers les énergies renouvelables, selon lequel, grâce à l'amélioration de l'efficacité énergétique des processus de production, serait possible une croissance économique plus rapide que l’augmentation de la consommation d’énergie primaire (découplage "relatif"), voire même avec une diminution de la consommation d’énergie primaire (découplage "absolu"). La limite à cette thèse du découplage est illustrée par le fait que les éoliennes modernes ont déjà atteint la limite physique de conversion imposée par la loi de Betz.
Et ce n'est pas tout : il apparaît en outre que le taux de retour énergétique de l'éolien et du solaire est généralement plus faible que celui des combustibles fossiles, notamment en raison des infrastructures décentralisées inhérentes à ces énergies renouvelables [source] ...
Régulation
Selon le chimiste Frederick Soddy, prix Nobel de chimie en 1921, la production de monnaie devrait être liée à celle d'énergie libre. Cela pourrait-il être réalisé au moyen d'un système bi-monétaire tel qu'une monnaie (disons "yang") serait utilisée pour les ressources matérielles (biens) et/ou "non-renouvelables" (pétrole, forêts, ...), et l'autre (disons "yin") pour les ressources immatérielles (services) et/ou renouvelables (énergie solaire, ...) ?
Selon Roddier la théorie du ruissellement d'Adam Smith n'est pas vérifiée en période de décroissance économique parce qu’une monnaie unique reste piégée dans les « puits de potentiel » que sont les placements financiers ou immobiliers. Une deuxième monnaie permet d’abaisser les « barrières de potentiel » de ces puits, et ainsi d’investir à long terme pour trouver de nouvelles ressources. En termes de cycles la monnaie "yin" est nécessaire pour refermer le cycle économique, comme une source froide est nécessaire pour refermer le cycle de Carnot [source]. En termes d'efficience l’usage de deux monnaies différentes dont on peut faire varier le taux de change, permet d’ajuster la barrière de potentiel économique qui sépare deux économies, comme un régulateur. Selon Roddier on pourrait procéder en conservant la monnaie en euros ("yang") pour l’achat de biens matériels, et en utilisant une nouvelle monnaie (yin) pour la nourriture, les salaires et les services. [source].
Équilibre
Lorsqu'on étudie la thermodynamique et les systèmes (mécaniques, biologiques, ...) on est inéluctablement conduit à faire une distinction entre système "à l'équilibre" et système "hors équilibre". La notion d'équilibre est importante notamment en physique, chimie et économie, car elle constitue un référentiel par rapport auquel on peut observer un changement. Intuitivement l'équilibre est associé à l'absence de changement.
1. Corps à l'équilibre2. Système à l'équilibre
3. Système complexe
Corps à l'équilibre
Définitions
Un corps est dit « à l'équilibre » si son accélération est nulle, c-à-d lorsqu'il est soit au repos (équilibre statique), soit en mouvement à vitesse constante (équilibre dynamique).
L'équilibre est la situation d'un corps ne subissant aucune force (ou dont la résultante des forces est nulle) dans un référentiel inertiel.
Un corps est en équilibre stable (statique ou dynamique) si, à la suite d'une perturbation qui a éloigné le système de son état initial, celui-ci y retourne spontanément. Dans le cas contraire l'équilibre est dit instable [source].
Exemple
Ainsi si l'on imprime une série de chocs de force croissante aux systèmes du graphique suivant (qui est un modèle d'équilibre statique), il arrivera un moment où la bille quittera définitivement sa position initiale, d'abord dans le système de droite (où seules les forces de frottement maintiennent la bille à l'équilibre), ensuite dans celui du milieu, et enfin dans celui de gauche.
En économie classique l'équilibre est caractérisé par l'égalité entre offre et demande, et le niveau de prix et quantité correspondants. Mais à quelles situations correspond alors, en économie, les notions d'équilibre stable et d'équilibre instable ?
Système à l'équilibre
Définitions
Il convient de distinguer les systèmes selon qu'ils sont ouverts ou fermés. Un système est fermé/isolé s'il ne peut échanger d'énergie (chaleur, travail mécanique, ...) avec le reste du monde, de sorte que son énergie interne est constante.
Les propriétés dynamiques respectives sont alors les suivantes :
- les systèmes fermés tendent vers l'équilibre statique c-à-d le repos, et cela en se déstructurant (augmentation de l'entropie) ; l'équilibre thermodynamique correspond au maximum d'entropie du système et à une distribution uniforme de l'énergie qu'il contient : toute différence de température disparaît, et toute activité mécanique cesse ;
- les systèmes ouverts peuvent tendre vers un équilibre dynamique s'ils sont traversés par un flux d'énergie continu et suffisant ; dans ce cas apparaissent des structures ordonnées et composées de flux d'énergie (qui sont périodiques dès lors que le flux d'énergie entrante/sortante est constant) ; on arrive à l'équilibre thermodynamique par diminution d'entropie jusqu'à un niveau nécessairement inférieur à son maximum (qui correspond à l'équilibre statique).
Exemples
Équilibre statique. Roddier cite l'exemple d'un système consistant en un mélange d'eau et de glaçons dans une bouteille thermos. Les glaçons vont fondre et la température de l'eau va s'uniformiser. L'entropie augmente et atteint son maximum à l'équilibre thermodynamique c-à-d lorsqu'il n'y a plus de différences de températures et donc plus de transferts de chaleur dans le système.
Équilibre dynamique. Roddier cite l'exemple d'un système constitué d'une casserole sur le feu et remplie d'eau. Au début la chaleur va se propager de bas en haut, sans provoquer de mouvement : c'est la conduction. Mais au delà d'un certain différentiel (gradient) de température entre le fond et le haut de la casserole, la conduction va se transformer en convection : un certain nombre de molécules acquièrent suffisamment de vitesse pour entrer dans une région plus froide sans être substantiellement ralenties ⇒ elles provoquent des collisions en chaînes. Plus chaude que l'eau ambiante, l'eau impliquée dans ces collisions est aussi moins dense ⇒ elle subit une poussée d'Archimède vers le haut, qui accélère leur mouvement. Il se produit alors une boucle de convection : l'au chaude monte à la surface, et s'y refroidit, de sorte qu'elle redescend (par les régions excentrées c-à-d là où la température est plus basse), et le cycle se poursuit tant que la chaleur injectée dans le système ne diminue pas. En raison de la forme de la casserole un courant d'eau en trois dimension va donc se former, dont le sens est de bas en haut et du centre vers l'extérieur, de sorte que le courant décrit un tore.
 Apparition d'une structure ordonnée, prévisible et en activité.
Apparition d'une structure ordonnée, prévisible et en activité.
- Alors que dans l'induction le flux de chaleur est proportionnel au différentiel vertical de température (⇒ le régime de dissipation de l'énergie est dit "linéaire"), dans la convection il est proportionnel au carré de ce différentiel (⇒ le régime de dissipation de l'énergie est dit "non linéaire").
- D'autres systèmes peuvent être caractérisés par d'autres types de gradient : de pression, de concentration chimique, etc.
Question de
vocabulaire ?
En fait Roddier ne parle pas d'équilibre dynamique. Il semble en effet réserver la notion d'équilibre thermodynamique au seul cas d'équilibre statique, c-à-d caractérisé par l'absence de tout mouvement mécanique : « Nous avons vu que l'état d'équilibre thermodynamique est celui d'entropie maximale. L'énergie mécanique y est uniformément distribuée entre tous les degrés de liberté du système, ce qui signifie : répartie au hasard entre toutes les molécules : le désordre y est le plus complet » [source p. 81]. Ainsi Roddier ne parle pas d'équilibre dynamique mais dit que « pour maintenir un système thermodynamique hors équilibre il faut lui apporter un flux d'énergie. Lorsque ce flux est constant le système atteint un état de régime permanent, qualifié d'état stationnaire » [source p. 75]. Autrement dit, dans le vocabulaire de Roddier, les systèmes ouverts tendent au déséquilibre thermodynamique (c-à-d au mouvement), éventuellement en se structurant (et dans ce cas l'entropie interne du système diminue).
Quoi qu'il en soit, à l'éventuelle diminution interne de l'entropie correspond nécessairement une augmentation au moins égale de l'entropie à l'extérieur du système observé. Ce système, dissipant de l'énergie, produit donc de l'entropie, mais cette dernière est évacuée aussi vite qu'elle est produite.
Exemple. Une plante absorbe de l'énergie sous forme de lumière solaire, qu'elle utilise pour construire des sucres, mais d'autre part elle éjecte de la lumière infrarouge, une forme d'énergie beaucoup moins concentrée. L'entropie globale de l'univers augmente pendant la photosynthèse alors que se dissipe la lumière du soleil, mais la plante maintient sa structure interne en ordre, l'empêchant de se délabrer, ou du moins retardant ce processus inéluctable.
Les tableau suivant synthétise les notions que nous venons de développer.
Typologie des systèmes
| Système fermé | Système ouvert | |
|---|---|---|
| Dynamique | Tend au repos (atteint à "l'équilibre thermodynamique") | Ne tend pas au repos (le système est "maintenu hors équilibre thermodynamique) |
| Organisation | Se désorganise (ses constituants se répartissent de façon aléatoire) |
|
| Entropie | Son entropie augmente jusqu'à son niveau d'équilibre |
|
| Information | Son contenu informationnel diminue |
|
| Évolution | Son évolution est prédictible |
|
Source : francois-roddier.fr (p. 11 et 12).
- Dans la source mentionnée ci-dessus Roddier semble dire que tous les systèmes ouverts sont dissipatifs, c-à-d (selon ma compréhension) que pour tout système ouvert il existe un niveau de flux d'énergie au-delà duquel apparaissent des structures dissipatives.
- Concernant la dernière ligne du tableau je crois comprendre que l'imprédictibilité mentionnée dans la dernière ligne (colonne de droite) est liée à la nature des systèmes complexes ⇒ effet papillon (cf. section suivante) ⇒ des structures permanentes apparaissent mais on ne peut prévoir lesquelles ...
Paradoxe ?
L'univers dans son ensemble - le plus grand des systèmes - est par définition considéré comme un système fermé : il n'existerait pas de milieu extérieur à lui-même avec lequel il pourrait échanger de l'énergie. Mais si l'univers est fermé comment expliquer son activité (dont la prolifération d'organismes vivants) ? L'explication que l'on a imaginée pour résoudre ce paradoxe est qu'en raison de l'expansion de l'univers et du caractère fini de la vitesse de la lumière il existe un horizon cosmique délimitant un univers observable, considéré comme ouvert sur la partie non observable de l'univers située au-delà de l'horizon cosmique. On sait aujourd’hui, note Roddier, « que l’univers observable perd sans cesse de la matière. Une partie de celle-ci disparaît derrière l'horizon cosmologique tandis qu’une autre partie disparaît à l’intérieur de trous noirs. En conséquence, l’entropie de l’univers observable peut fort bien diminuer. L’apparition spontanée de différences de température, lors de la formation des étoiles, laisse à penser que c’est le cas » [source].
Système complexe
Irréversibilité
et déterminisme
Nous avons vu que tous les phénomènes physiques sont fondamentalement irréversibles irréversibles, c-à-d que, sauf effet du hasard, les systèmes inertes comme vivants ne retrouvent généralement pas spontanément leur état immédiatement antérieur à une modification. On observe certes des fluctuations aléatoires d’entropie telles que celle-ci diminue occasionnellement, mais jamais en valeur moyenne. Il en résulte que la reconstitution de la trajectoire passée d'un corps (comète, électron, ...) à partir de l'observation d'une période de sa trajectoire ne serait "exacte" que par approximation probabiliste. Cette limitation vaut également pour la prédiction de sa trajectoire future. Tout cela ne remet cependant pas en cause le déterminisme scientifique : la nature obéit bien à des lois strictes, immuables et parfaitement identifiables. Les technologies fonctionnent bien, et cela malgré des (voire au moyen d') approximations dans leur conception.
Ordre vs prévisibilité. Qui dit apparition dʼordre dit apparition dʼinformation nouvelle, donc de phénomènes imprévisibles (un phénomène prévisible n'apporte pas d'information nouvelle) [source].
Déterminisme
et complexité
Cette problématique prend cependant une autre dimension dans le cas des systèmes dynamiques complexes (c-à-d non linéaire et avec un grand nombre de degrés de liberté), et sensibles aux conditions initiales, tels que les phénomènes météorologiques (mais aussi économiques ...). Dans ce cas, modélisé par la théorie du chaos, des différences infimes dans les conditions initiales peuvent entraîner des résultats fortement différenciés, rendant en général toute prédiction impossible à long terme (effet "papillon"). Cependant il n'y a pas indéterminisme au sens que « des causes identiques produiraient des effets différents », mais identification incomplète et mesure imparfaite des paramètres. Il n'y a donc pas remise en cause du déterminisme, mais plutôt des limites de son utilisation : cette limitation de nos capacités de mesure est-elle surmontable par le progrès scientifique et technologique, ou bien constitue-t-elle une impossibilité physique ? Selon le principe d’incertitude de Heisenberg il y a bien une limitation physique insurmontable : toute amélioration de la précision de mesure de la position d’une particule se traduit nécessairement par une moindre précision de mesure de sa vitesse et vice-versa.
Sensibilité aux conditions initiales

Dans cette animation en boucles (30 sec.), après quelques secondes les deux pendules se désynchronisent brusquement [source].
Roddier constate que « le phénomène non linéaire de sensibilité aux conditions initiales remet en cause l’idée de déterminisme et nécessite une révision de la notion de causalité. Les biologistes s’aperçoivent aujourd’hui que les gènes coévoluent avec leur environnement sans qu’il y ait nécessairement une relation de cause à effet » [source].
Application
économique
Le modèle d'équilibre général sur lequel repose la théorie économique classique, qui décrit une économie de "marchés parfaits", est déterministe, prédictible et mécanique. Mais cette approche réductionniste n'est pas pertinente pour les systèmes complexes. Ce qui est le cas du système économique, évolutif et organique, plutôt qu'en situation "d'équilibre", même instable (oscillations).
Création monétaire. Ainsi la théorie du chaos confirme un principe de base du financement distributif de l'AU selon lequel la croissance de la création monétaire devrait être constante. Autrement dit la théorie du chaos infirme la thèse selon laquelle "l'autorité monétaire" (la Banque centrale) serait en mesure d'adapter rationnellement la masse monétaire aux besoins de l'économie, que ce soit pour seulement contrôler l'inflation ou en outre stimuler la croissance (politique monétaire dite "adaptative", par assouplissement ou restriction monétaire).
Structure dissipative
Le physicien François Roddier situe ainsi le phénomène : Les structures dissipative s'auto-organisent spontanément et décrivent des cycles semblables à ceux des machines thermiques. Or tout ensemble de molécules ou d'organismes vivants interagissant entre eux et parcouru par un flux permanent d'énergie peut être considéré comme un réseau neuronal, et donc comme une structure dissipative [source p. 17-18]. L'on comprend alors la portée de cette notion de structure dissipative, que nous allons ici approfondir.
Lorsqu’un système reçoit un flux continu d’énergie, ce flux permet l’apparition de « structures dissipatives » mises en évidence par Ilya Prigogine (université libre de Bruxelles), prix Nobel de chimie en 1977. On parle de « structure dissipative » dans le cas d'un système ouvert ne pouvant subsister (état stationnaire) que s'il est traversé par des flux d'énergie. Une structure dissipative est donc un système hors équilibre : son énergie interne reste constante (comme dans un système fermé) mais elle est constamment renouvelée (contrairement à un système fermé) [source].
Maximisation. Des physiciens ont émis l'hypothèse que ces structures/systèmes tendraient à maximiser les flux d'énergie qui les traversent, ou plus précisément la vitesse à laquelle ils dissipent de l'énergie et partant "produisent de l'entropie". Si cette hypothèse - que semble confirmer l'observation des phénomènes naturels - était en outre démontrée mathématiquement on aurait alors une nouvelle interprétation du troisième principe de la thermodynamique (cf. supra #energie-principes) – concernant les systèmes ouverts – et appelé principe d'entropie maximale : l’énergie tend à se dissiper le plus vite possible, compte tenu des contraintes.
Auto-organisation. Pour François Roddier les système thermodynamiques hors équilibre s'auto-organisent, mais de façon difficile à prévoir [source p. 14]. Les structures dissipatives s’auto-organisent pour maximiser ( N.D.L.R. : "en maximisant" ?) le flux permanent d’énergie qui les traverse, cela en mémorisant de l’information sur leur environnement.
Maximisation "out" et minimisation "in". Maximiser une quantité implique souvent d’en minimiser une autre. Ainsi une structure dissipative minimise son entropie interne pour en maximiser sa production externe d'entropie. Plus est élevé le flux d'énergie qui traverse constamment une structure dissipative, plus la structure s'auto-organise c’est-à-dire diminue son entropie (ou désordre) interne, mais aussi plus elle produit d’entropie. Pour maintenir son état ordonné (d’entropie faible), elle doit constamment évacuer l’entropie qu’elle produit vers son environnement. Ainsi l’entropie qu’exportent les structures dissipatives équivaut à une importation d’information sur leur environnement.
- Ordre. L’ordre peut être défini comme une façon de mémoriser l’information. Ainsi on met de l’ordre dans un atelier pour y retrouver les outils » [source].
- Information. Fondamentalement, une information est une modification d’un système induite par son environnement et qui subsiste ensuite, même si l’environnement évolue. Appliquez une force sur une boule de billard. Elle va se mettre en mouvement. Supprimez la force. La boule de billard va continuer à rouler. Elle a mémorisé de l’information. S’il y a des frottements, la boule de billard va finir par s’arrêter. L’information s’efface progressivement. Cette perte d’information est irréversible, à l'instar de la dissipation de l’énergie [source].
Selon le physicien Per Bak les structures dissipatives s'organisent à la manière des transitions de phase continues, comme le passage de l’état liquide à l’état solide, c-à-d au passage d’un état désordonné (l’état liquide) a un état ordonné (l’état cristallin).
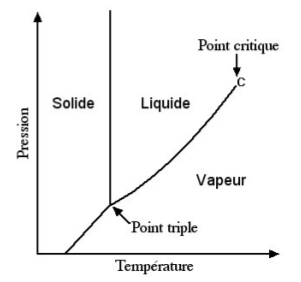
« Au delà du point critique il n'y a plus de différence entre l'état liquide et l'état gazeux. Il est possible de passer continûment de l'état liquide à l'état gazeux en contournant le point critique. Le passage direct de l'état liquide à l'état gazeux comme l'ébulition, où son inverse la condensation de l'eau, s'appelle une transition de phase abrupte. Les transitions abruptes comme l'ébulition nécessitent un apport de chaleur sans qu'il y ait augmentation de température, tandis que la condensation de l'eau produit un dégagement de chaleur. La chaleur ainsi échangée porte le nom de chaleur latente. Lorsque le corps est très pur, la transition ne s'effectue pas spontannément. Un «germe» est nécessaire pour la déclencher. On met souvent un peu de sel dans l'eau pour faciliter l'ébullition. Au point critique la chaleur latente s'annule. On parle alors de transition continue. Le point critique est un point où le fluide est extrêmement instable. Il se condense de lui-même pour former un brouillard appelé opalescence critique. Ce brouillard a la propriété d'avoir le même aspect à l'œil nu, à la loupe ou au microscope. On dit qu'il est invariant par changement d'échelle » [source].
Lorsque l’instabilité au point critique se manifeste, un fluide se divise en phases, une phase “vapeur”, une phase “liquide”. Les structures dissipatives oscillent constamment de part et d’autre de leur point critique, à partir duquel une fluctuation aléatoire peut déclencher une avalanche d’événements. Des avalanches de bifurcations produisent des arborescences fractales : amplification des fluctuations --> rupture de symétrie (avec invariance par changement d'échelle) --> apparition et mémorisation d'information. C’est le processus de "criticalité auto-organisée", ayant pour caractéristique de produire des fluctuations dites en 1/f, dont l’amplitude est inversement proportionnelle à la fréquence f (il y a beaucoup de petites avalanches, de temps en temps des plus grosses, exceptionnellement des très grosses).
On pourrait donc caractériser les structures dissipatives en trois points [source] :
- elles ne subsistent que traversées par un flux permanent d'énergie ;
- elles tendent à maximiser le flux d'énergie qui les traverse ;
- elles s'auto-organisent en suivant des cycles de transformations.
« Plus une structure dissipative mémorise dʼinformation, plus elle dissipe dʼénergie. Mais plus vite elle dissipe de lʼénergie, plus vite elle modifie son environnement, de sorte que lʼinformation quʼelle mémorise devient peu à peu obsolète. La structure dissipative a de plus en plus de mal à dissiper lʼénergie. Pour continuer à le faire, elle doit se restructurer. Elle a atteint un point dit "critique" à partir duquel lʼinformation mémorisée se restructure constamment suivant un mécanisme dʼavalanches » [source].
Application
biologique
Selon le physicien François Roddier, en biologie l'ontogenèse correspondrait à une transition abrupte [exemple], et la phylogenèse à une transition continue. Les transitions abruptes nécessitent un apport extérieur d’information sous la forme d’un germe (N.d.A. : discontinuité de la fonction entropie ?). Quant à la transition continue elle n'est pas déclenchée par un germe mais par un ensemble de conditions (température et pression) appelé "point critique". Lors des transitions continues – cas des structures dissipatives – de l’information apparaît progressivement au fur et à mesure que la phase ordonnée se développe (N.d.A. : continuité de la dérivée première de la fonction entropie ?). Ces informations se propagent par percolation au sein de domaines d'Ising.
Dans le cas des espèces vivantes, le point critique correspond à la transition entre ce que les biologistes appellent la sélection K et la sélection r. Lorsque l'environnement est stable, la sélection naturelle favorise les espèces les mieux adaptées. C'est la sélection K. Elle favorise les espèces qui dissipent le plus d'énergie, par exemple chez les grands arbres ou les grands mammifères (rigidité du chêne, espèce adaptée). Mais ceux-ci modifient leur environnement qui va peu à peu évoluer. La sélection naturelle va alors favoriser les espèces non plus les mieux adaptées mais les plus adaptables, celles qui sont capables de s'adapter le plus rapidement à un nouvel environnement, comme dans la savane ou chez les petits mammifères. C'est la sélection r (souplesse du roseau, espèce adaptable) [source].
Application
économique
Cycles économiques. « Une société humaine est un organisme vivant. Son métabolisme est l’économie. Il est donc naturel que celle-ci soit constituée de cycles autour d’un point critique ». Le point critique est un point d’équilibre entre offre et demande. Le décalage entre l’offre et la demande est ce qu’en physique on appelle l’hystérésis. Les cycles économiques d’hystérésis sont selon Roddier le moteur de l’économie. « On peut comparer l’économie à un cyclone. La partie en équilibre est l’œil du cyclone, un point de calme plat. Un cyclone se renouvelle constamment en aspirant l’air tout autour. Il ne traverse pas de crise particulière ».
Régulation. « De même, il faudrait pouvoir renouveler l’économie de façon continue. C’est ce que font les ingénieurs dans un moteur d’automobile. On ne construit pas un moteur à un seul cylindre. On en met au moins deux en opposition de phase, de préférence quatre en quadrature. (...) On répartit ainsi les phases de crises tout autour du cycle.
Imprévisibilité. Cependant « à l’instar des êtres vivants, les cyclones sont constamment à la recherche de nourriture, en l’occurrence le moindre gradient de température. Leur trajectoire est imprévisible. (...) Les systèmes auto-organisés sont parcourus par un flux permanent d’énergie et oscillent autour d’instabilités critiques. Ce ne sont pas des points critiques statiques, mais des points critiques dynamiques. (...) L’évolution économique de l’humanité aura toujours un certain caractère imprévisible » [source].
Notons que ce fait infirme la thèse selon laquelle "l'autorité monétaire" (la Banque centrale) serait en mesure d'adapter rationnellement la masse monétaire aux besoins de l'économie, que ce soit pour seulement contrôler l'inflation ou en outre stimuler la croissance (politique monétaire dite "adaptative", par assouplissement ou restriction monétaire). Ainsi l'approche thermodynamique de l'économie confirme la thèse de la théorie relative de la monnaie selon laquelle la création monétaire devrait être constante (cf. article sur le financement distributif de l'AU). La fonction d'un système bimonétaire "yin/yang vise à minimiser l'amplitude de cycles imprévisibles.
https://allocation-universelle.net/thermodynamique#biologie-economie
Information
Commençons par rappeler les notions que nous avons évoquées jusqu'ici au sujet du concept d'information :
- l’irréversibilité thermodynamique provient du passage de l’ordre au désordre, et cette dégradation correspond à une perte d'information sur la trajectoire particulière de chacune des particules. L'entropie est donc une mesure de notre perte/manque d'information concernant l'état microscopique d'un système observé.
- Toute perte d'information est liée à une opération irréversible.
- Qui dit apparition dʼordre dit apparition dʼinformation nouvelle, donc de phénomènes imprévisibles (un phénomène prévisible n'apporte pas d'information nouvelle).
- Pour maximiser le flux d’énergie qui les traverse les structures dissipatives s’auto-organisent, et cela en mémorisant/important de l’information sur leur environnement.
- L'entropie qu’exportent les structures dissipatives équivaut à une importation d’information sur leur environnement.
- L'ordre peut être défini comme une façon de mémoriser l'information. Ainsi on met de l’ordre dans un atelier pour y retrouver les outils.
- Fondamentalement, une information est une modification d’un système induite par son environnement et qui subsiste ensuite, même si l’environnement évolue. Appliquez une force sur une boule de billard. Elle va se mettre en mouvement. Supprimez la force. La boule de billard va continuer à rouler. Elle a mémorisé de l’information. S’il y a des frottements, la boule de billard va finir par s’arrêter. L’information s’efface progressivement. Cette perte d’information est irréversible, à l'instar de la dissipation de l’énergie.
- Plus une structure dissipative mémorise dʼinformation, plus elle dissipe dʼénergie. Mais plus vite elle dissipe de lʼénergie, plus vite elle modifie son environnement, de sorte que lʼinformation quʼelle mémorise devient peu à peu obsolète. La structure dissipative a de plus en plus de mal à dissiper lʼénergie. Pour continuer à le faire, elle doit se restructurer. Elle a atteint un point dit "critique" à partir duquel lʼinformation mémorisée se restructure constamment suivant un mécanisme dʼavalanches.
- Les transitions abruptes nécessitent un apport extérieur d’information sous la forme d’un germe. Lors des transitions continues – cas des structures dissipatives – de l’information apparaît progressivement au fur et à mesure que la phase ordonnée se développe. Ces informations se propagent par percolation au sein de domaines d'Ising.
- Concluons cette liste par une judicieuse observation : « Il ne va pas de soi, étant donné l’usage habituel du mot information, que la notion d’information dans la théorie du même nom se rapproche plus de la notion courante d’incertitude que de celle d’information » [source]. L'information n'est donc pas un stock mais un flux : l'information que nous avons sur l'état d'un système augmente lorsque diminue l'incertitude quant cet l'état.
Selon Roddier l'équivalence (au signe près) entre entropie et information est démontrée car :
- la théorie de l'information de Shannon montre que l'entropie est un cas particulier d'information ;
- le principe de Landauer montre que l'information est un cas particulier d'entropie.
Roddier rappelle que « évacuer de l’entropie signifie importer de l’information. Une structure dissipative importe sans cesse de l’information de son environnement. Lorsqu’elle s’auto-organise une structure dissipative diminue son entropie interne, donc augmente son contenu en information en la mémorisant. C’est une mémoire temporaire. En régime stationnaire, une structure dissipative perd autant d’information qu’elle en mémorise. Elle renouvelle sans cesse l’information qu’elle mémorise. Perdre de l’information est synonyme de produire de l’entropie, donc de dissiper de l’énergie. C’est en effaçant continuellement de l’information qu’elle a mémorisée qu’une structure dissipative dissipe de l’énergie. S’il est naturel de parler de diminution d’entropie lorsqu’une machine thermique comme un cyclone s’auto-organise, parler d’information mémorisée est plus inhabituel. La mémoire d’un cyclone est inertielle. Si vous coupez la source d’énergie, le cyclone va continuer à tourner mais de moins en vite. La mémoire de ce mouvement va s’effacer progressivement au fur et à mesure que l’énergie se dissipe ». De même, en vieillissant nos capacités de mémorisation diminuent avec notre capacité physique à dissiper de l'énergie [source].
Roddier énonce trois principes caractérisant l'information [source] :
- est information tout ce qui peut être mémorisé ;
- l'information induit un délai entre un événement et ses conséquences ;
- la surface déterminée par un cycle d'hystérésis mesure la quantité d'énergie dissipée (entropie).
Application
économique
La monnaie utilisée, mesure de néguentropie du système économique. Selon le physicien François Roddier la monnaie elle-même peut être considérée comme une mesure d’entropie ou plutôt de son opposé appelé néguentropie (ou entropie négative). La monnaie a notamment pour fonction de maintenir la réversibilité des échanges. Tout ce qui se dégrade, perd de la valeur monétaire (son entropie augmente). Inversement une chose précieuse est généralement une chose rare donc de faible entropie. C’est ainsi que le prix du pétrole augmente lorsque la probabilité d’en trouver diminue [source].
Roddier voit également la monnaie comme un catalyseur, à l'instar des enzymes : un organisme vivant fonctionne avec “des cycles de réactions chimiques grâce à des catalyseurs", quant à l’économie elle fonctionne en effectuant “des cycles d’échanges avec des devises différentes”.
Un principe de base du financement distributif de l'AU est que l'aspect qualitatif de la monnaie est liée au principe de symétrie spatio-temporelle de son allocation (création monétaire constante et partage égale et gratuit entre tous les citoyens).
Travail intellectuel
Roddier fait remarquer que « notre cerveau rationnel obéit à notre cerveau affectif. Cherchant à maximiser notre bien-être, ce dernier obéit à notre cerveau reptilien qui lui-même obéit à nos gènes. Enfin ces derniers obéissent aux lois de la chimie c’est-à-dire, in fine, de la thermodynamique » [source].
Dans la mesure où le travail intellectuel relève de processus chimiques, et est par conséquent déterminé au niveau microscopique de particules ou de très petites molécules, quelques questions viennent naturellement à l'esprit. Ainsi peut-on parler de "travail" intellectuel dès lors que le travail est défini par l'accélération d'une masse sur une certaine distance ... ? Le "travail" intellectuel consiste-t-il en des interactions entre particules ? Il semble que oui. Mais alors quels sont les effets du principes d'incertitude sur notre conception du travail intellectuel ?
Roddier note que « il est plus satisfaisant de dire que l'entropie d'un système dépend de l'information qu'on a sur ce système, mais beaucoup de physiciens refusent encore de donner à l'entropie ce caractère subjectif. Il me parait cependant nécessaire, si l'on veut conserver le libre arbitre et la possibilité de faire des choix éthiques. Bien que subjective au niveau individuel, l'entropie reste objective au niveau de la société. Elle est parfaitement mesurable de manière statistique » [source].
Ces questions se posent avec d'autant plus d'acuité que, selon l'état actuel des connaissances en physique quantique, il semble qu'en-dessous d'une taille charnière située entre les niveaux moléculaire et atomique les lois naturelles seraient différentes de celles observées au niveau macroscopique [vidéo de vulgarisation].
Pourtant, le global/macro étant composé du local/micro, on pourrait s'attendre à une cohérence d'intégration entre les deux niveaux ...
Indétermination quantique. À noter cependant cette absence apparente de cohérence entre relativité générale et mécanique quantique ne se manifeste que lorsque l'observateur est (ou s'est mis) dans l'incapacité d'identifier - parmi plusieurs comportements possibles des particules - celui va déclencher la mesure du phénomène observé ... (situation dite d'indétermination quantique) [vidéo de vulgarisation].
La réponse à ces questions sera peut-être donnée par la théorie de l'information quantique dont un principe fondamental est que la quantité d'information "contenue dans" un événement dépend de sa probabilité : plus un événement est improbable ex-ante, plus l’information que sa réalisation apporte ex-post est élevée. Aux limites cette quantité d'information est nulle lorsque l’événement est certain (probabilité = 1) ou impossible (probabilité = 0), et maximale lorsque sa probabilité vaut 1/2. Il en résulte que l'entropie évoquée plus haut constitue une mesure (au signe près) de la quantité d'information "contenue dans" un événement (par exemple le résultat d'une expérience de physique).
Entropie et information, exemple concret. Roddier cite l'exemple suivant : vous pouvez soit ranger vos outils en mettant de l’ordre soit les laisser en désordre et mémoriser l’information sur leur emplacement. Si vous perdez cette information l’entropie augmentera et il vous faudra dépenser de l’énergie pour les retrouver.
Pour le mathématicien René Thom « (...) toute information est d'abord une forme, et la signification d'un message est une relation de caractère topologique entre la forme du message et les formes caractéristiques du récepteur (c'est-à-dire les formes susceptibles de provoquer une excitation du récepteur) ; réduire l'information à sa mesure scalaire (évaluée en bits), c'est réduire la forme à sa complexité topologique (...), c'est pratiquement tout oublier de son caractère signifiant » [source].
Le risque est la mesure de l'incertitude, il mesure la probabilité de réalisation ou non réalisation d'un événement futur incertain. Le secteur des assurances a développé toute une économie basée sur la gestion du risque.
Intelligence collective. Chez les organismes vivants, l'information est essentiellement mémorisée dans les gènes et transmise génétiquement (ainsi les espèces animales ou végétales peuvent être vues comme des domaines d’Ising. Chez les humains, elle est principalement mémorisée dans le cerveau et transmise par le langage. Les sociétés humaines ont pu se développer grâce à une nouvelle forme de mémorisation et de transmission de l’information: l’écriture. C’est ce qu’on appelle la "culture". Les individus qui partagent la même culture forment les domaines d’Ising que sont les sociétés humaines. Les lois de la thermodynamiques expliquent donc aussi le phénomène sociologique d'auto-organisation [source1, source2].
Évolution. Plus une structure dissipative mémorise d'informations plus elle dissipe d'énergie. Cependant il y a une différence de nature fondamentale entre énergie et information : la première se conserve tandis que la seconde peut être répliquée. C'est pourquoi, selon le physicien Eric Chaisson, l'univers créerait sans cesse de nouvelles structures dissipant l'énergie plus efficacement que les anciennes. Ainsi une espèce vivante maximiserait sa dissipation d'énergie en s'adaptant - toujours plus vite - à son environnement. Se fondant sur la distinction faite par l'éthologiste Richard Dawkins entre mèmes et gènes, le généticien Cavali-Sforza constate que, chez l'Homo sapiens, l'évolution culturelle (technique) est plus rapide que l'évolution génétique [source].
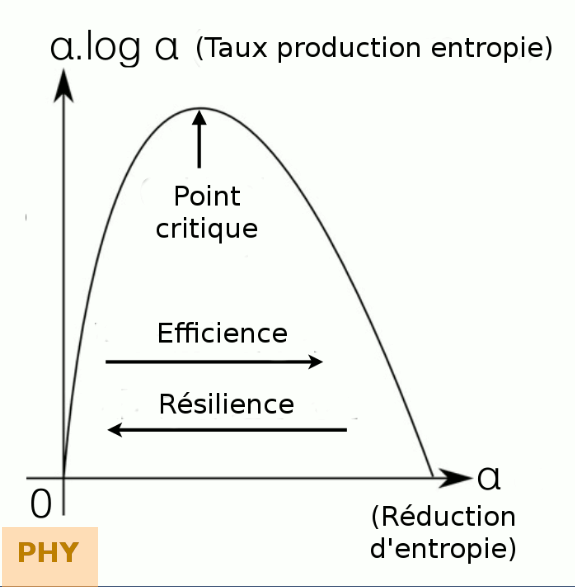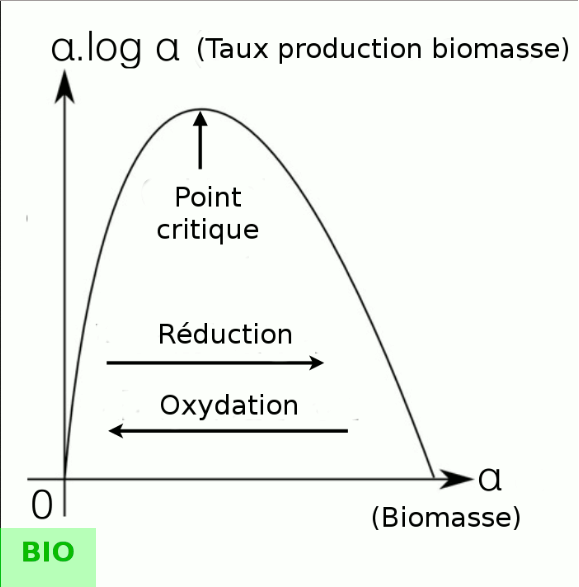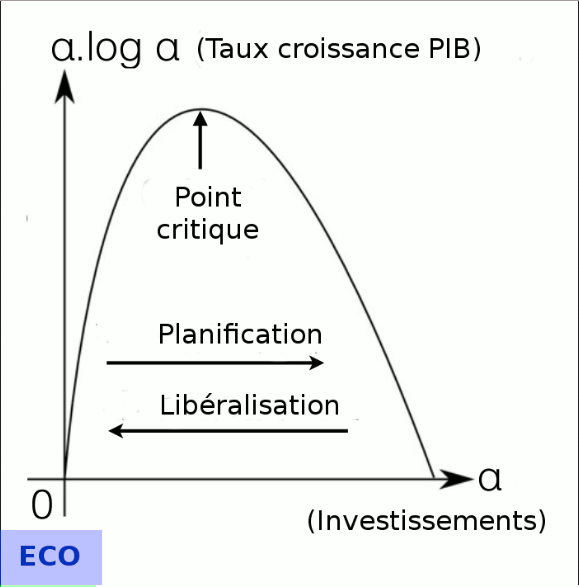
Ce GIF animé montre en cycle les interprétations physique, biologique et économique [source].
Stationnarité optimale. Selon l'ingénieur-chimiste Robert Ulanowicz plus la quantité d’information qu'elle mémorise est grande, mieux une structure dissipative s’adapte à son environnement, mais plus elle doit modifier d’information pour rester adaptée, donc plus elle dissipe d’énergie. Il arrive un moment ou la fraction de mémoire disponible devient insuffisante, de sorte que les capacités d’adaptation de la structure n’augmentent plus et même diminuent. Il existerait une valeur de la fraction de mémoire utilisée (α) pour laquelle la capacité d’adaptation est optimale. Ulanowicz définit la robustesse R d’un écosystème comme étant sa capacité à s’adapter aux changements. Il montre que R doit être de la forme R = -α.log(α). La robustesse est nulle pour α = 0 et pour α = 1. Elle est maximale et égale à 1 pour α = 1/e où e est la base des logarithmes népériens (e = 2,718) [source].
Approfondir : https://democratiedirecte.net/intelligence
Tous les articles du dossier Travail :