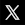VII.2. Financement distributif
Résumé
N.B. Il est vivement recommandé de précéder la lecture du présent document par celle de /financement-synthese.

Désintermédiation monétaire
Le financement distributif de l'AU (AUD, soit environ 16 % de l'AU) est constitué par la création monétaire. La monnaie est créée à taux relativement constant (seulement fonction de l'espérance de vie de la zone monétaire), et distribuée également et gratuitement entre les seules personnes physiques :
AUD = ΔM / N ≈ 4 / v * Mt-1 / Nt où :
- v est l'espérance de vie (dans la zone monétaire considérée) ;
- M la masse monétaire M3 ≈ 15.500 milliards en zone euro [2021 Q4 : source] ;
- 4 / v est une approximation du taux de croissance universel/naturel de la monnaie, soit 5,6 % en zone euro (2021) ;
- N la population de la zone monétaire (342 millions en zone euro).
Nous avons donc que AUD = 0,056 * 15.500 / 0,342 ≈ 2.550 euros/ans ≈ 200 euros/mois en zone euro en 2021.
La proposition/découverte du taux de croissance universel de la monnaie par l'ingénieur Stéphane Laborde en 2011 dans sa "théorie relative de la monnaie" (TRM) apporte une solution à la situation actuelle caractérisée par des politiques monétaires arbitraires aux motivations souvent occultes et douteuses, qui ne sont pas étrangères à l'instabilité monétaire (dont les bulles spéculatives) qu'elles sont supposées neutraliser.
Pas de création monétaire supplémentaire. Actuellement la monnaie est créée par les banques et distribuée par elles de façon arbitraire à des personnes physiques comme morales, via des crédits avec intérêts (donc remboursables et payants). Dorénavant la monnaie créée serait distribuée gratuitement et à parts égales entre les citoyens (donc uniquement à des personnes physiques). Ce seraient alors uniquement ceux-ci qui par leur consommation détermineraient désormais ce qui doit être produit, les banques perdant le pouvoir d'orienter la production via la part de la création monétaire allouée par elles aux entreprises (PS : les banques conservent cependant leur fonction d'intermédiaire entre prêteurs et emprunteurs, mais perdent le pouvoir de création et allocation monétaire, ce qui implique que leur coefficient de réserve doit être de 100% des crédits).
Dans le système monétaire actuel plus de 90% de la monnaie est créée par les banques. Il s'agit donc de monnaie privée, et c'est bien pour cela qu'elles sont en mesure de ne prêter que contre intérêt malgré que la monnaie est créée ex-nihilo.
Théorie relative
de la monnaie
Le financement distributif de l'AU est une application de la théorie relative de la monnaie (TRM) proposée au début des années 2010 par l'ingénieur français Stéphane Laborde. La TRM propose un nouveau système monétaire fondé sur le principe de symétrie spatio-temporelle. Le fonctionnement des systèmes monétaires ne devrait avantager aucun individu ni aucune génération : tous les individus et générations devraient être égaux devant la création, allocation et utilisation monétaire.
La TRM suggère que, pour respecter le principe de symétrie spatio-temporelle, la monnaie doit être :
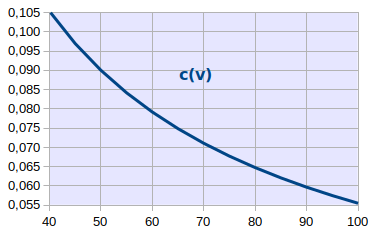
créée à un taux de croissance (c) relativement constant, seulement fonction de l'espérance de vie (v)<--> symétrie temporelle :
c ≈ 4 / v
distribuée également entre tous les citoyens ; <--> symétrie spatiale :
Ut = ΔMt / Nt = c * Mt-1 / Nt où :
- Ut est appelé dividende universel (DU dans le texte)
- Mt = masse monétaire, Nt = population
utilisable inconditionnellement (gratuité, facilité d'utilisation, code source ouvert)<--> symétrie spatiale :
Par "principe de relativité monétaire" on entend que :
la valeur attribuée à un bien/service varie selon les individus (dimension spatiale), ainsi qu'au cours du temps pour un même individu (dimension temporelle) ;
le respect de cette subjectivité – c-à-d la relativité du jugement de valeur par le (ou par rapport au) référentiel qu'est l'individu humain – requiert une forme d'invariance au niveau de la création, allocation & utilisation monétaire : la création monétaire devrait être relativement constante, et allouée également et inconditionnellement entre tous les citoyens (principe de symétrie monétaire).
Pas de monnaie libre. Le financement distributif de l'AU est une application modifiée de la théorie relative de la monnaie. En effet Laborde ne conçoit l'application de la TRM qu'au seul cas de "monnaies libres", qui sont des monnaies locales (en tous cas au début de leur existence) et gérées en réseau décentralisé. Le problème est que les monnaies locales échouent généralement après quatre ou cinq ans (cf. /creation-monetaire#monnaies-locales-limitations), et les monnaies libres en particulier posent en outre certains problèmes (cf. /monnaie-directe#limitations). Dans notre modèle le financement distributif de l'AU n'est donc pas fondé sur des monnaies libres mais sur l'application du principe de symétrie spatio-temporelle aux monnaies nationales. C'est pourquoi nous parlons alors plutôt de "monnaie directe" plutôt que de "monnaie libre".
Voyons maintenant en détails les principes que nous venons de résumer.
Révision sur les taux de croissance
Quelques rappels mathématiques, qui s'avéreront très utiles pour la compréhension des développements mathématiques concernant le financement distributif de l'AU ...
1. Taux effectif2. Taux intrinsèque
3. Synthèse
4. Applications
Taux effectif
taux
discret
Le taux de croissance discret ct d'une grandeur M entre les instants t-1 et t se calcule comme suit :
ct = (Mt - Mt-1) / Mt-1 ⇔
ct = ( Mt / Mt-1 ) - 1 ⇔
- Ce taux est dit "discret" car il concerne deux valeurs successives d'une série de mesures.
- Le taux de croissance entre Mt-1 et Mt peut être noté ct-1 ou ct. C'est juste une convention, mais une fois déterminée il faut s'y tenir. Nous avons donc choisi ct.
Si on isole Mt dans le membre de gauche, on peut alors exprimer sa valeur en fonction de Mt-1 et du taux de croissance subi par ce dernier.
Mt = (1+ct) * Mt-1
taux
moyen
On peut alors trouver la formule du taux de croissance moyen entre deux instants quelconques (donc pas nécessairement successifs dans une série de valeurs), par itérations du taux de croissance discret :
- M1 = ( 1 + c1 ) * M0
-
M2 = ( 1 + c2 ) * M1 ⇔
M2 = ( 1 + c2 ) * ( 1 + c1 ) * M0 ⇒
si c1 = c 2 = c ⇒ M2 = ( 1 + c ) 2 * M0 -
M3 = ( 1 + c3 ) * M2 ⇔
M3 = ( 1 + c3 ) * ( 1 + c )2 * M1 ⇒
si c3 = c ⇒ M3 = ( 1 + c ) 3 * M0 - etc ...
dont on déduit que :
Mt = Mt-n * (1+c) n ⇔
et par conséquent le taux moyen c sur la période entre t=0 et t=n est tel que :
c = ( Mt / Mt-n ) 1/n - 1
NB : constatez que le taux discret ct n_ct=(Mt/Mt-1)-1 est un cas particulier du taux moyen c n_c=(Mt/Mt-n)exp(1/n)-1 où n=1 !
Taux intrinsèque
Le taux de croissance intrinsèque (ci ) est une approximation à la limite du taux de croissance effectif, c-à-d donnant une valeur acceptable ... pour autant que c soit suffisamment petit. Il présente l'avantage de simplifier certains calculs.
Nous avons obtenu le taux effectif moyen des taux discrets par un développement déductif. Nous allons ici obtenir le taux intrinsèque par intégration des taux discrets.
Mt = (1+ct) * Mt-1 n_Mt=(1+ct)*Mt-1 ⇔
Mt - Mt-1 = ct * Mt-1 ⇒
si c est petit ⇒
Mt - Mt-1 ≈ ct * Mt
que l'on peut récrire en utilisant la notion de différentielle :
dMt / dt ≈ ct * Mt ⇔
dMt / Mt ≈ ct * dt
⇒ intégration avec remplacement de la variable ct par la moyenne c :
∫ 1 / Mt * dMt ≈ ∫ c * dt ⇔ (primitive)
ln(Mt) ≈ c * t + k
où k est une constante arbitraire ⇒
on trouve la valeur de k en posant t = 0 ⇒ k = ln(M0) ⇒
ln(Mt) ≈ c * t + ln(M0) ⇔
c ≈ ln( Mt / M0 ) / t
où le membre de droite est appelé "taux intrinsèque de croissance moyenne", et noté ci :
On a juste remplacé l'indice 0 par t-n ⇒ le dénominateur t=n
ci = 1 / n * ln ( Mt / Mt-n )
Et l'on obtient le taux discret à partir du taux moyen en posant n=1 dans n_ci=1/n*ln(Mt/Mt-n) ⇒
cit = ln ( Mt / Mt - 1 )
Enfin on pourra exprimer Mt en fonction de ci à partir de n_ci=1/n*ln(Mt/Mt-n) ⇒
Mt = Mt-n * e ci * n
dont on exprimera la version discrète en posant également n=1 dans n_Mt=Mt-n*eexp(ci*n) ⇒
Mt = Mt-1 * e ci
Équivalence
On peut montrer, de diverses façons, qu'il existe une relation d'équivalence entre taux intrinsèque et effectif :
c = e ci - 1
Première démonstration :
n_ci=1/n*ln(Mt/Mt-n) ci = 1 / n * ln ( Mt / M0 ) ⇔
e ci = ( Mt / M0 ) 1 / n ⇔
e ci - 1 = ( Mt / M0 ) 1 / n - 1 ⇔ par n_c=(Mt/Mt-n)exp(1/n)-1 :
e ci - 1 = c
CQFD
Seconde démonstration (à la limite) :
∀ c : limc→0 c = limc→0 ec - 1 = 0 ⇔
si c est petit ⇒ c ≈ ec - 1
CQFD
Il en résulte que ∀ c suffisamment petit 1+c ≈ ec ⇔ c ≈ ln(1+c) ⇔ ln(x) ≈ x - 1.
Synthèse
Le premier tableau à deux entrées rassemble les quatre formules du taux de croissance.
| Effectif | Intrinsèque (si c petit) | |
|---|---|---|
| Moyen | c = ( Mt / Mt-n ) 1/n - 1 n_c=(Mt/Mt-n)exp(1/n)-1 | ci = 1 / n * ln ( Mt / Mt - n ) n_ci=1/n*ln(Mt/Mt-n) |
| Discret | ct = ( Mt / Mt-1 ) - 1 n_ct=(Mt/Mt-1)-1 | cit = ln ( Mt / Mt-1) n_cit=ln(Mt/Mt-1) |
Le lecteur constatera que dans les deux cas on passe :
- de l'effectif à l'intrinsèque (de gauche à droite dans le tableau) en remplaçant x - 1 par ln x
- du moyen au discret (de haut en bas dans le tableau) en remplaçant n par 1 (et c par ct ).
Mémorisation : il suffit de retenir les deux formules du taux moyen, puisque celles du taux discret n'en sont qu'un cas particulier.
Exercice de mémorisation des taux moyen. Dans c = ( Mt / Mt-n ) 1/n - 1 n_c=(Mt/Mt-n)exp(1/n)-1 et ci = 1 / n * ln ( Mt / Mt - n ) n_ci=1/n*ln(Mt/Mt-n) comparez la place de Mt / Mt - n et de 1 / n. Puis, avec l'aide cette information, écrivez par coeur les deux équations.
Indice initial : 0 ou 1 ?
Si dans le cas "Moyen" on pose n = t - 1 alors la ligne devient :
| Moyen | c = ( Mt / M1 ) 1/(t-1) - 1 n_c=(Mt/Mt-n)exp(1/n)-1 | ci = 1 / (t-1) * ln ( Mt / M1 ) n_ci=1/n*ln(Mt/Mt-n) |
|---|
Si on pose plutôt n = t alors la ligne "Moyen" devient :
| Moyen | c = ( Mt / M0 ) 1/t - 1 n_c=(Mt/Mt-n)exp(1/n)-1 | ci = 1 / t * ln ( Mt / M0 ) n_ci=1/n*ln(Mt/Mt-n) |
|---|
La notation n = t - 1 correspond donc à l'attribution du temps t=1 à la première valeur de la série historique, tandis que la notation n = t revient à lui attribuer la valeur zéro. Mais ces deux notations sont équivalentes : ainsi les formules ne doivent pas être adaptées puisque dans les deux cas le x du coefficient 1 / x est toujours la différence entre l'indice du numérateur et l'indice du dénominateur du ratio My / Mz.
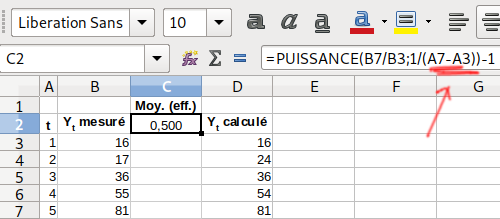
Pour éviter tout risque de confusion l'image suivante montre comment procéder dans un tableur.
Indice du temps dans un tableur
Le second tableau à deux entrées rassemble les quatre formules en isolant Mt.
| Effectif | Intrinsèque (si c petit) | |
|---|---|---|
| Continu | Mt = Mt - n * ( 1 + c ) n n_Mt=Mt-n*(1+c)expn | Mt = Mt-n * e ci * n n_Mt=Mt-n*eexp(ci*n) |
| Discret | Mt = Mt-1 * ( 1 + ct ) n_Mt=(1+ct)*Mt-1 | Mt = Mt-1 *e cit n_Mt=Mt-1*eexpci |
Le lecteur constatera que dans les deux cas on passe :
- de l'effectif à l'intrinsèque (de gauche à droite dans le tableau) en remplaçant ( 1 + c ) par e ci
- du continu au discret (de haut en bas dans le tableau) en remplaçant n par 1 (et c par cit ).
Mémorisation : il suffit de retenir les deux formules de l'approche continue, puisque celles de l'approche discrète n'en sont qu'un cas particulier.
Exercice de mémorisation. Dans Mt = Mt - n * ( 1 + c ) n n_Mt=Mt-n*(1+c)expn et Mt = Mt-n * e ci * n n_Mt=Mt-n*eexp(ci*n) comparez la place de Mt / Mt - n et de 1 / n. Puis, avec l'aide cette information, écrivez par coeur les deux équations.
Indice initial : 0 ou 1 ?
Si dans le cas "Continu" on pose n = t - 1 alors la ligne devient :
| Continu | Mt = M1 * ( 1 + c ) t-1 n_Mt=Mt-n*(1+c)expn | Mt = M1 * e ci * (t - 1) n_Mt=Mt-n*eexp(ci*n) |
|---|
Si on pose plutôt n = t alors la ligne "Continu" devient :
| Continu | Mt = M0 * ( 1 + c ) t n_Mt=Mt-n*(1+c)expn | Mt = M0 * e ci * t n_Mt=Mt-n*eexp(ci*n) |
|---|
Ces deux notations sont également équivalentes, sauf si vous êtes amenés à calculer un logarithme de t (NB : ln(0) n'existe pas), par exemple pour une courbe de régression. Il est donc recommandé de préférer la notation n = t - 1 et donc d'attribuer le temps t=1 à la première valeur des séries historiques.
Applications des taux de croissance
Deux très utiles applications des formules que nous venons de développer sont le passage en taux de croissance, et les courbes de régression.
Passage en taux
de croissance
Les propriétés de la fonction logarithme permettent le passage d'une égalité statique en une égalité dynamique, c-à-d où les variables sont exprimées en taux de croissance. Mais ce passage n'est valable que si les taux de croissance sont suffisamment proches de zéro.
Soit :
Y = P * Q
où :
Y : PIB
P : Prix
Q : production
Soit Y', P' et Q' des valeurs proches de respectivement Y, P et Q, alors :
Y/Y' ≈ P/P' * Q/Q' ≈ 1 ⇒
ln(Y/Y') ≈ ln(P/P' * Q/Q') ≈ ln(1) = 0 ⇒ par la propriété d'un produit de logarithme :
ln(Y/Y') ≈ ln(P/P') + ln(Q/Q') ≈ ln(1) = 0 ⇒ par ci = 1 / n * ln ( Mt / Mt - n ) n_ci=1/n*ln(Mt/Mt-n) :
y ≈ p + q ≈ 0
où y, p et q sont les taux de croissance de Y, P et Q.
Courbe de
régression
Le tableur du graphique suivant montre que les quatre formules permettent de calculer une même courbe de régression (rouge) pour les valeurs mesurées (bleu). Les valeurs de la courbe rouge sont donc calculées, et la courbe qu'elles forment est une approximation lissée de la courbe (bleue) des valeurs mesurées.
La courbe de régression exponentielle calculée par le tableur (en vert) est différente car une méthode différente est utilisée (voir aussi wikipedia.org/wiki/Régression_(statistiques)). Elle constitue manifestement une régression plus précise que celle calculée au moyen de nos formules.
Cette révision salutaire sur les taux de croissance s'achève ici. Entrons maintenant dans le vif du sujet, par la formalisation des conditions de symétrie spatio-temporelle dans la TRM.
Symétrie spatio-temporelle
2. Symétrie temporelle
Symétrie spatiale
Le principe de symétrie spatiale postule que pour traiter également les utilisateurs vivants d'une monnaie, la création monétaire doit être partagée également entre les membres de la zone monétaire.
On appelle "dividende universel" (DU dans le texte, Ut dans les formules) ce montant distribué à chaque citoyen.
Ut = ( M t - M t-1 ) / N t
où Mt et Nt sont respectivement la masse monétaire et la population à l'instant t (telle année, tel mois ou tel jour, selon l'échelle temporelle utilisée).
En y substituant M t - M t-1 = c t * M t-1 n_ct=(Mt/Mt-1)-1 on obtient :
Ut = c t * M t-1 / N t
où ct est le taux de croissance de Mt-1 à Mt
Forme continue. L'équation n_Ut=ct*Mt-1/Nt présente Ut sous forme discrète (c-à-d entre deux périodes consécutives). On pourrait aussi considérer sa forme continue (c-à-d par rapport à une période de base t=0), exprimée en fonction du taux de croissance moyen (effectif ou intrinsèque). Pour ce faire il suffit de substituer Mt = M0 * (1+c) t n_Mt=Mt-n*(1+c)expn ou Mt ≈ M0 * e c * t n_Mt=Mt-n*eexp(ci*n) dans n_Ut=ct*Mt-1/Nt qui devient alors :
Ut = ct * (1+c) (t-1) * M0 / Nt
ou encore, par approximation à la limite pour c proche de zéro :
Ut ≈ ct * e c * (t-1) * M0 / Nt
Exercice : expliquez la différence entre ct et c dans ces deux formules.
Symétrie temporelle
1. Formulation2. Démographie
Formulation
Le principe de symétrie temporelle postule que le taux de croissance monétaire doit être constant : ct = c de sorte que Ut = c t * M t-1 / N t n_Ut=ct*Mt-1/Nt devient :
Ut = c * M t-1 / N t
Il reste cependant à déterminer la valeur de cette constante, ce qui revient implicitement à considérer l'existence d'un taux de croissance naturel/universel de la monnaie ...
Pour ce faire l'auteur de la TRM fait une analogie entre une fontaine et la succession des générations dans le temps :
- le débit constant du jet d'eau exprime la croissance monétaire ;
- le temps qu'il faut à chaque goutte d'eau pour parcourir le jet d'eau exprime l'espérance de vie (82 ans dans la zone euro, et que nous allons noter v ).

 Jusque là, rien à redire. Cependant, Laborde fait alors un "passage en force" en déduisant de cette analogie – comme si c'était une évidence – que « nous pouvons donc poser comme relation fondamentale que la création de la masse monétaire durant toute l’espérance de vie passée ne doit être représentée à " t " vis-à-vis de la masse monétaire existante que par la petite fraction des individus de cette génération presque totalement disparue mais encore présente dans la hauteur temporelle en proportion de 1/ev » [source]. Autrement dit :
Jusque là, rien à redire. Cependant, Laborde fait alors un "passage en force" en déduisant de cette analogie – comme si c'était une évidence – que « nous pouvons donc poser comme relation fondamentale que la création de la masse monétaire durant toute l’espérance de vie passée ne doit être représentée à " t " vis-à-vis de la masse monétaire existante que par la petite fraction des individus de cette génération presque totalement disparue mais encore présente dans la hauteur temporelle en proportion de 1/ev » [source]. Autrement dit :
Mt / Mt+v = 1 / v ⇔
Mt+v / Mt = v ⇔
Mt / Mt-v = v ⇔
De sorte que par Mt = Mt-n * (1+c) n n_Mt=Mt-n*(1+c)expn :
1 / (1 + c ) v = 1 / v ⇔
c = v 1/v - 1
Nous appelons c, le taux universel de croissance monétaire (TUCM).
Formule simplifiée. Nous avons vu que si c est suffisamment petit alors 1+ c ≈ e c n_c=eexpci-1 ⇒ n_c=vexp(1/v)-1 peut être reformulé comme suit :
ec = v 1/v ⇔
c = ln (v 1/v) ⇔ par clipedia-txt.net/mesure#n_logdepuissance ;
c = ln(v) / v
Mais revenons à n_Mt/Mt+v=1/v : pourquoi constitue-t-elle un "passage en force" ? On peut éventuellement comprendre que l'on pose par exemple Mt+v / Mt = vt+v / vt (PS : ce qui donnerait un très faible taux de croissance monétaire ...) qui compare deux taux de variation (plutôt qu'un taux avec une valeur absolue ...) et qui repose sur un postulat qui fait sens : la croissance monétaire est liée au développement économique, qui lui même influence l'espérance de vie. Mais Mt+v / Mt = v cela fait-il sens ? Force est de constater que Laborde n'avance aucun argument pour justifier le saut de l'analogie vers l'égalité n_Mt/Mt+v=1/v. Tout au plus exprime-t-il une intuition.
Pour justifier l'intuition de Laborde (que nous partageons) cherchons à définir une grandeur x¯ et une fonction f() telles que :
- c = f(x¯) ;
- f() reflète la croissance économique ;
- x¯ reflète le niveau de développement économique ;
- x¯ a le plus faible taux de croissance parmi les grandeurs qui vérifient la condition précédente (notion d'invariance relative) ;
- f() soit la plus simple possible (cf. rasoir d'Ockham).
Les critères 1 et 2 sont vérifiés par:
f ( x¯ ) = Mt / Mt-Δ ⇒ par n_Mt=Mt-n*(1+c)expn :
f ( x¯ ) = ( 1 + c ) Δ ⇔
c = f ( x¯ ) 1/Δ - 1
Il nous reste donc à trouver quelque chose pour x¯ et f().
En proposant x¯ = v il semble que nous vérifions les critères 3 et 4.
x¯ = v --> c = f ( v ) 1/Δ - 1
Enfin le principe 5 est vérifié en posant :
- f(x) = x --> c = v 1/Δ - 1
v est donc un point fixe.
- Δ = v --> c = v 1/v - 1
Nous sommes ainsi arrivés à c = v 1/v - 1 n_c=vexp(1/v)-1 en argumentant chaque étape du raisonnement. On peut certes critiquer certaines d'entre elles mais elles ont au moins le mérite d'exister et d'ainsi constituer un référentiel stimulant la réflexion et le débat.
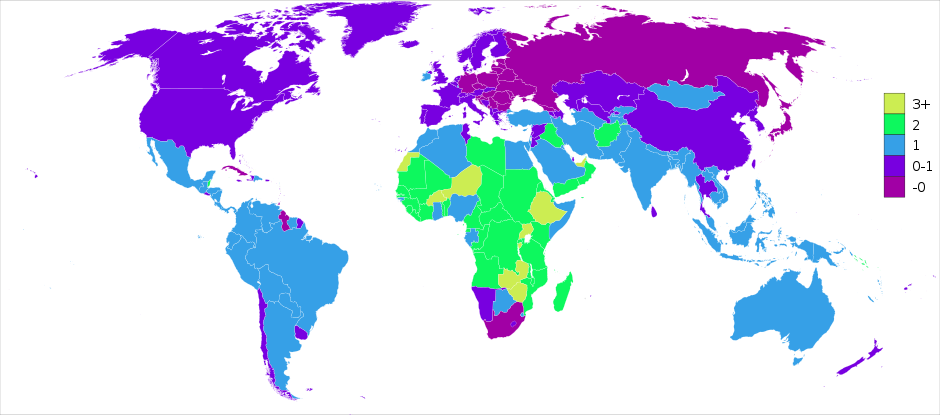
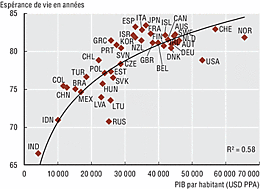
Notons enfin une propriété remarquable de n_c=vexp(1/v)-1 : le taux universel de croissance monétaire (TUCM) est plus élevé dans les pays dont l'espérance de vie est plus faible (donc dans les pays moins développés).
Espérance de vie
L'espérance de vie à la naissance est une grandeur moyenne calculée annuellement sur base des taux de mortalité par âge, et qui suppose que ces taux demeurent constants durant la vie des individus [source].
L'espérance de vie varie dans le temps (durant la vie d'un individu) et dans l'espace (selon les pays) en fonction notamment du niveau scientifique et de développement économique.
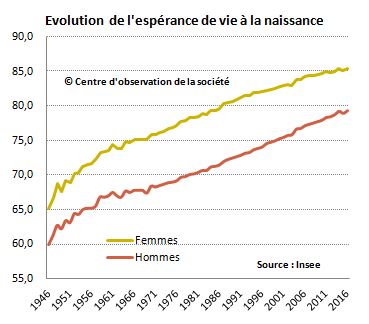
Le tableau suivant montre que l'espérance de vie en France a grimpé d'une vingtaine d'année au cours des sept dernière décennies, soit une progression moyenne de 0,4 %/an. Cependant l'espérance de vie en bonne santé progresse environ quatre fois moins vite. Elle est ainsi de 63 ans en France (2016), n'ayant augmenté que de 0,1 %/an en moyenne entre 2004 et 2016 [source].
Analyse temporelle (source : Insee)
Analyse spatiale (source : Wikipédia)
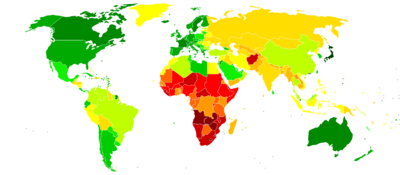
≥ 70 ans
|
< 70
|
Espérance de vie et PIB/hab (source : OCDE)
Démographie
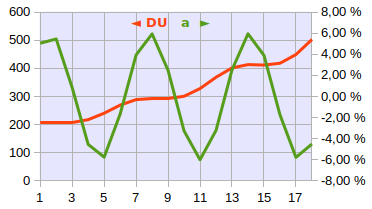
Le graphique suivant montre la sensibilité relative du DU (dividende universel, en rouge) par rapport aux variations de N (a, taux de croissance de la population, en vert) : Nt = (1+at) * Nt-1 n_Mt=(1+ct)*Mt-1.
Pour analyser mathématiquement l'effet de a sur le DU il suffit de substituer Mt = (1+c) * Mt-1 et Nt = (1+at) * Nt-1 n_Mt=(1+ct)*Mt-1 dans Ut = c * M t-1 / N t n_Ut=c*Mt-1/Nt ⇒
Ut = c * ( 1 + c ) * Mt-2 / [ ( 1 + at ) * Nt-1 ] ⇔
Ut = ( 1 + c ) / ( 1 + at ) * c * Mt-2 / * Nt-1 ⇔
Ut = ( 1 + c ) / ( 1 + at ) * Ut-1 ⇒
Ut / Ut-1 = ( 1 + c ) / ( 1 + at ) < 1 ⇔
Ut / Ut-1 = ( 1 + c ) / ( 1 + at ) < 1 ⇔
le DU baisse dès que at > c c-à-d dès que la population croît à un taux supérieur à celui de la création monétaire (résultat que l'on pouvait deviner intuitivement).
En quoi les variations du DU sont-elles problématiques ? Des baisses importantes et imprévues du DU, par exemple suite à une vague d'immigration pourrait mettre en difficulté des personnes n'ayant que l'AU comme seul revenu.
Dans la zone euro l'espérance de vie v≈81 [source] de sorte que n_c=vexp(1/v)-1 c = v 1/v - 1 = 81 1/81 - 1 = 5,6 %. Or le taux de croissance de la population de la zone euro fut en moyenne de 0,2% par an entre 2012 et 2022 [source], ce qui est très inférieur à 5,6%.
Ainsi on s'aperçoit donc que, du point de vue de l'économie politique, le principe de symétrie temporelle de la création monétaire (c-à-d création à taux relativement constant, fonction de la seule espérance de vie) ne fait sens que si l'on se situe dans le cas d'une population relativement constante c-à-d faiblement variable (a < c).
Par conséquent il convient ici de bien faire la distinction selon que le financement distributif de l'AU (Rappel : AU=AUD+AUR) est réalisé :
- soit avec la monnaie officielle (on parle alors de "monnaie directe", par opposition aux "monnaies libres" de l'option suivante) ⇒ pas de problème car le taux de croissance de la population nationale est faible;
- soit avec des monnaies libres (monnaies locales, à cours libre et en réseau décentralisé) ⇒ la problématique est nettement plus complexe car la variation de la population des membres d'un système monétaire libre est généralement nettement plus variable d'une année à l'autre (pouvant même changer de signe) et d'une valeur absolue plus élevée. C'est particulièrement le cas durant sa période d'installation, qui peut durer de nombreuses années. Ainsi une monnaie libre dont le nombre des utilisateurs croît rapidement peut voir son DU baisser de façon vertigineuse, de sorte que ceux qui sont entrés les premiers dans la monnaie ont reçu durant leurs premières périodes une somme d'argent nettement plus élevée que ce que recevront les nouveaux membres (et les anciens) durant une période de même durée. Le principe de symétrie n'est alors plus respecté ...
Monnaie directe vs libre
Dans la théorie relative de la monnaie (TRM) son auteur Stéphane Laborde ne considère l'application de la TRM qu'au seul cas de monnaies locales à cours libre et gestion décentralisée, ce qui l'amène à :
définir la notion de monnaie libre ;
considérer que le référentiel de la TRM n'est pas l'espérance de vie (v) mais la demi-espérance de vie (qu'il appelle "centre de symétrie") de sorte que c = v 1/v - 1 n_c=vexp(1/v)-1 devient c = ( v / 2 ) 2/v - 1
Selon Laborde il convient de diviser l'espérance de vie afin de prendre en compte le fait qu'on peut "entrer dans la monnaie libre" à n'importe quel âge. Dans le cas d'une monnaie nationale qui serait distribuée également et intégralement entre les personnes physiques (nous parlons alors de "monnaie directe") le cas se présente moins souvent puisque, exception faite des immigrés, la plupart des utilisateurs de la monnaie sont membres du système monétaire depuis leur naissance.
énoncer que la valeur de c est autorisée à fluctuer entre deux valeurs extrêmes, dont la valeur supérieure correspondrait au ... centre de symétrie (???) ;
remplacer Ut = c * M t-1 / N t n_Ut=c*Mt-1/Nt par Ut+1 = Ut + c2 * Mt-1 / Nt afin d'empêcher que le DU puisse baisser sous l'effet d'une hausse de la population des membres de la monnaie libre (PS : il en résulte une explosion du taux de croissance monétaire) ;
interpréter le phénomène de convergence en des termes dont le manque de précision et la confusion peuvent faire croire (i) que l'effet de convergence (cf. infra) serait spécifique aux monnaies libres, (ii) que les valeurs supérieures et inférieures de c correspondraient à des propriétés spécifiques.
Le tableau suivant synthétise les principales différences entre les deux versions de la TRM selon que celle si est appliquée aux monnaies libres ou à la monnaie nationale (nous parlons alors de monnaie directe).
| TRM appliquée à : | Monnaie nationale (monnaie directe) | Monnaie libre |
|---|---|---|
| Sym. spatiale | Ut = c * M t-1 / N t n_Ut=c*Mt-1/Nt | Ut+1 = Ut + c2 * Mt-1 / Nt |
| Sym. tempor. | c = v 1/v - 1 n_c=vexp(1/v)-1 | c = ( v/2 ) 2/v - 1 n_c=(v/2)exp(2/v)-1 |
Systèmes
monétaires
symétriques
La monnaie directe est la monnaie nationale créée et intégralement distribuée symétriquement par l'État (la Banque centrale) entre les personnes physiques. Une monnaie libre est par contre gérée par les citoyens sans passer par l'intermédiaire des banques ce qui implique que les systèmes monétaires libres doivent être capables de conférer de façon 100% décentralisée et sans l'intervention de l'État, une valeur d'usage monétaire à la monnaie libre, et cela sans reproduire in fine une autre forme de banques privée, de Banque centrale et d'État ...
Le tableau suivant synthétise les différences entre systèmes monétaires symétriques selon qu'ils sont fondés sur une monnaie directe (c-à-d) nationale ou libre (c-à-d locale). La dernière ligne montre l'arbitrage que les systèmes monétaires visant à appliquer le principe de symétrie spatio-temporelle sont contraints d'opérer en raison de la difficulté (voire l'impossibilité ?) d'obtenir un système monétaire 100 % symétrique (dans le cas des réseaux décentralisés, notamment en raison du théorème CAP).
| Monnaie directe | Monnaie libre | ||
|---|---|---|---|
| Symétrie | Création | à taux constant | à taux constant |
| Allocation | égalitaire | égalitaire | |
| Utilisation | inconditionnelle c-à-d :
|
libre au niveau de :
|
|
| Application | Cours | légal | libre (c-à-d non légal) |
| Réseau | maximisation de la décentralisation sous contrainte de 100% symétrique |
maximisation de la symétrie sous contrainte de 100% décentralisé |
Une "voie du milieu" consiste à entendre par "État" et "Banque centrale", non plus les institutions actuellement connues sous ces dénominations, mais un méta-réseau décentralisé et composé de réseaux locaux centralisés, et dont les organisations qui en constituent les noeuds sont des coopératives publiques, le tout dans un État fonctionnant en démocratie directe telle que définie par democratiedirecte.net.
Valeur de c et Ut
2. Montant du DU
Valeur de c
Dans la zone euro l'espérance de vie v≈81 [source] de sorte que n_c=vexp(1/v)-1 c = v 1/v - 1 = 81 1/81 - 1 = 5,6 %.
Formule simplifiée : c = ln(v) / v n_c=ln(v)/v ⇒ c = ln(81) / 81 = 5,4 %
À titre de comparaison, sur la période 1999-Q1 (année de création de l'euro) à 2023-Q3, le taux de croissance annuel de M3 dans la zone euro fut en moyenne de ... 5,5 % ! [source].
Cette égalité avec c apporte de l'eau au moulin des thèses selon lesquelles les ajustements monétaires opérés par les Banques centrales – selon des critères arbitraires et obscures – participent aux phénomènes d'instabilité monétaire qu'elles sont supposées neutraliser. Le tabeau suivant qui montre les fluctuations du taux de croissance monétaire autour de sa tendance en est une parfaite illustration.
Dans le cas de monnaies libres, le taux de croissance monétaire est plus élevé : n_c=(v/2)exp(2/v)-1 c = ( v/2 ) 2/v - 1 = 9,6 %
Problème du
changement
d'unité
Il y a cependant un problème avec les équations n_c=vexp(1/v)-1 comme n_c=(v/2)exp(2/v)-1 : en raison de leur exposant (ou du logarithme si on l'exprime en taux de croissance intrinsèque plutôt qu'effectif) la valeur de c change significativement si l'on change simplement d'unité. Ainsi si l'on raisonne par exemple en jours plutôt qu'en années, alors "c" passe de 5,5 %/an à : (80*365) 1/(80*365) - 1 = 0,035 %/jour soit 1,00035365 - 1 = 13,7 %/an.
Soit "cd" et "cy" les taux effectifs de croissance journalière et annuelle et Mt la masse monétaire mesurée quotidiennement nous avons que :
M365 = (1 + cy ) * M0
M365 = (1 + cd ) 365 * M0
de sorte que
(1+cy)1 = (1+cd)365
La réponse de Laborde à cette objection est que l'activité économique serait rythmée par le cycle annuel des saisons (fait reflété par la comptabilité annuelle des entreprises et États), et que par conséquent ne pas fixer l'unité temporelle de la TRM sur la seule année tropique n'aurait pas de sens.
Notons à cet égard que le physicien François Roddier fait remarquer que la plupart des exemples d’effondrements de civilisations sont le fait de civilisations à moins de 35° de l’équateur, or plus on se rapproche de l'équateur moins les saisons sont marquées. Ces faits renforcent la thèse selon laquelle l'alternance de saisons serait un facteur de stabilité sociétale, par effet de synchronisation [source], ce que semble confirmer le moindre développement économique (mais aussi la meilleure préservation de l'écosystème ...) aux alentours de l'équateur [constater]. On peut donc voir c comme un taux de croissance naturel de la monnaie, déterminé par le cycle des saisons (facteur naturel) et l'espérance de vie (facteur humain).
Cependant les arguments de Laborde ne changent rien au fait qu'une année mesurée en jours demeure une année. Par conséquent pourquoi la valeur de c devrait-elle être fonction de l'unité choisie ? Les arguments de Laborde n'étant pas recevables, il faudrait trouver une autre formulation des équations n_c=vexp(1/v)-1 comme n_c=(v/2)exp(2/v)-1 de telle sorte que la valeur de c ne soit plus sensible au changement d'unité. Nous verrons plus loin l'ingénieuse (mais malheureusement imparfaite) réponse apportée par l'auteur de la TRM.
Montant du DU
On peut réécrire Ut = c * M t-1 / N t n_Ut=c*Mt-1/Nt en y injectant c = v 1/v - 1 n_c=vexp(1/v)-1 de sorte que :
Ut = ( v 1/v - 1 ) * M t-1 / N t
Avant de passer à l'évaluation de U2018 dans la zone euro, quelques mots sur la masse monétaire.
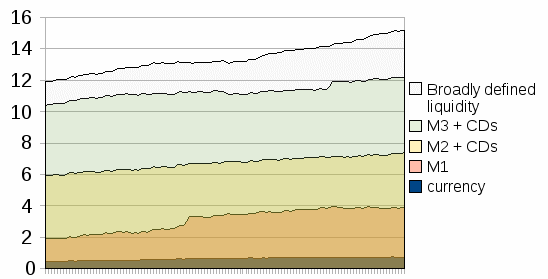
Pas de M4
alors 1,3*M3
Dans un article quelque peu confus, l'auteur de la TRM estime que l'application de la comptabilité en partie double aux produits financiers a pour effet de doubler la masse monétaire. Il cite pour exemple le fait que des agents économiques acceptent des Bons du Trésor comme moyen de paiement [source].
La remarque de Laborde n'est pas dénuée de fondement, bien qu'il est probable que les contreparties comptables d'actifs monétaires ne sont pas toutes des instruments de paiement. N'est-ce pas précisément la fonction des agrégats monétaires de M1 à M4 que d'incorporer uniquement celles qui le sont ? Ainsi M4 incorpore les Bons du Trésors cités en exemple par Laborde. Le problème c'est que la Banque centrale européenne ne calcule plus M4 et utilise M3 comme indicateur de la masse monétaire "large".
Parmi les BC qui calculent encore M4, il y a le Japon. Sur base des statistiques du Yen [source], on peut déduire une relation entre M4 et M3 :
M = 1,3 * M3
RSA. Laborde fait remarquer que si l'on calcule le montant du DU dans la zone euro, en fonction de 2*M3 plutôt que de M3 (et en calculant c en fonction de v/2) on obtient un DU du même ordre de grandeur que le RSA.
Il y aurait alors une opération à appliquer lors de l'initialisation du financement distributif de l'AU (que nous appelons aussi "monnaie directe") :
U1 = c * 1,3 * M30 / N1
On va supposer ici que le montant du DU est calculé une fois par an, divisé par douze puis distribué mensuellement (ce qui en pratique n'est sans doute pas la meilleure façon de procéder, mais l'objectif est ici de faciliter la compréhension de la TRM).
Une alternative consiste à (i) faire correspondre la période de calcul avec celle de distribution du DU, et (ii) de choisir la périodicité mensuelle. Il faut alors convertir le taux annuel en son équivalent mensuel par la formule (1+cy)1 = (1+cm)12 ⇔ cm = (1+cy)1/12 - 1 où "cm" et "cy" sont les croissances mensuelle et annuelle.
Dans la zone euro :
- population : N = 341 millions [1/1/2022 - source] ;
- croissance population : a = 0,2 %/an [moyenne 2012-2022 - source] ;
- espérance de vie : v = 81 [2019 - source] ;
- masse monétaire : M3 = 15.668 milliards € [2022 Q1 - source].
Il en résulte de n_Ut=(vexp(1/v)-1)*Mt-1/Nt et n_M=x*M3 que U2018 = ( 81 1/81 - 1 ) * ( 1,3 * 15.668 ) / 0,341 ≈ 3.330 euros/an ≈ 277 euros/mois par individu en 2022.
Cependant, nous allons finalement évaluer M par M3 plutôt que M4, car :
- l'approximation de M4 par n_U1=c*x*M30/N1 est beaucoup trop approximative ;
- il nous paraît plus cohérent de reproduire la "logique" appliquée par la BCE pour mesurer la masse monétaire de l'euro.
Par conséquent :
U2018 = ( 81 1/81 - 1 ) * 15.668 / 0,341 ≈ 2.562 euros/an ≈ 213 euros/mois par individu en 2022. Pour faciliter la mémorisation (et aussi puisque nous ne prétendons pas proposer autre chose que des ordres de grandeur), nous arrondissons à la cinquantaine : DU(=AUD)=200 euros/mois en 2022 dans la zone euro.
L'approche du MFRB. À titre de comparaison on notera que le Mouvement français pour un revenu de base (MFRB) estimait quant à lui (NB : en 2015) le montant du dividende monétaire (DM) de façon très différente. En partant d'une masse monétaire M1 de la zone euro à 5.000 milliards d'euros et en ciblant un taux de croissance de 5% (à comparer au taux de 6 à 10% observé lors de la dernière décennie) le MRFB propose la formule suivante : DM = (M1 x (A + i) x RO) / (12 x N) où A est le taux de croissance cible de M1 (5%), i le taux d'intérêt (5%), RO le taux de réserve obligatoire des banques (qui serait de 50%, contre 1% actuellement), et N la population concernée par le DM (250 millions d'équivalents adultes). Dans ces conditions DM = 83 euros/mois ... [source p. 174-175]. Ce chiffre est à comparer avec la valeur du DU en 2015, soit 150 euros/mois, et en se rappelant que DU≡AUD ne représente que 20% de l'AU !
Rappelons que le présent document concerne l'AUD (soit environ 16 % de l'AU), que nous appelons également "monnaie directe". Dans le cas d'une monnaie libre, le montant du DU est arbitraire puisqu'il dépend d'une masse monétaire initiale qui n'existe pas au moment de sa création. Si la monnaie libre est lancée par dix personnes, elles décident que le stock monétaire de départ est x de sorte qu'à la période 1 chacun recevra un DU = x / 10. À quel niveau faut-il fixer x ? Une solution consiste à le fixer de telle sorte que le DU de la monnaie libre soit égale à celui de la monnaie directe : 200 = x / 10 ⇔ x = 2.000 unités monétaires qu'ils peuvent appeler du nom qu'ils souhaitent (la june, notée Ğ1, dans le cas de monnaie libre créée par Laborde et son équipe de développeurs web) et dont le taux de change implicite avec l'euro serait alors de 1 june = 1 euro. En période 1 de la vie de cette nouvelle monnaie libre, la valeur du DU serait donc DU = 2.000 / 10 = 200 junes. Un marché du change june/euro pourrait être créé, de sorte que le taux de change évoluerait. Si le marché estime que l'avenir de la june est plus prometteur que celui de l'euro, alors la valeur de la june s'appréciera par rapport à celle de l'euro.
Convergence
2. Démonstration
3. Fiscalité redistributive
Principes
Préambule
Nous développons ici une propriété particulière des systèmes monétaires symétriques (monnaie directe ou monnaies libres), à savoir la convergence relative des écarts de richesse, que l'on peut formaliser en divisant les deux membres de Ut = c * M t-1 / N t n_Ut=c*Mt-1/Nt par la masse monétaire moyenne par individu Mt / Nt :
Ut / ( Mt / Nt ) = c * M t-1 / N t / ( Mt / Nt ) ⇔
Ut / ( Mt / Nt ) = c * M t-1 / Mt ⇒ par n_Mt=(1+ct)*Mt-1 :
Ut / ( Mt / Nt ) = c / ( 1 + c )
Ainsi donc, lorsque la création monétaire est constante le rapport entre le DU et la masse monétaire moyenne est constant. Oui, et alors ?, pourrait-on arguer : si dans le système monétaire actuel la création monétaire était constante (symétrie temporelle), on constaterait également que ( ΔMt / Nt ) / ( Mt / Nt ) = ΔMt / Mt = c / ( 1 + c ) c-à-d que le montant moyen de création monétaire par individu représenterait une part constante de la masse monétaire moyenne par individu !
C'est vrai, mais attention, il y a quand même une (grosse) différence : si en outre le principe de symétrie spatiale est vérifié (partage égalitaire, gratuit et inconditionnel de la crétion monétaire entre les seules personnes physique), alors la propriété n_Ut/(Mt/Nt)=c/(1+c) a pour implication que la part de création monétaire perçue par tout individu (le DU) représente un part constante de la masse monétaire moyenne par individu. Il en résulte le phénomène de convergence des inégalité de richesse que nous allons décrire.
Les systèmes monétaires symétrique ont d'autres effets économiques que la convergence. Nous le verrons lorsque nous étudierons la notion de champ de valeurs.
Énoncé
Si de façon récurrente la création monétaire était partagée également entre tous (AUD pour la monnaie directe, DU pour les monnaies libre), alors – abstraction faite des différences dans les capacités de chacun à faire fructifier cette rente monétaire – les différentiels de richesse diminueraient nécessairement.
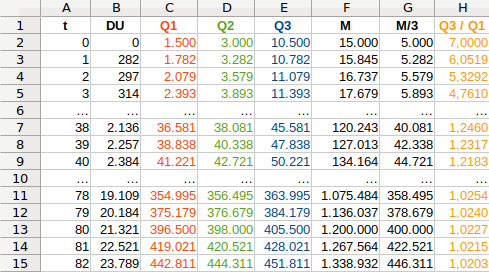
Le tableau suivant montre le cas de trois individus de patrimoines initiaux différents. La colonne Q3/Q1 mesure l'écart de richesse entre l'individu le plus fortuné et le moins fortuné : il diminue mois après mois (à supposer que le DU soit distribué mensuellement). Cela se comprend intuitivement par le fait que, avec l'accumulation des DU, la part du patrimoine initial de chacun diminue relativement au plus récent. Or, dès lors que les différents patrimoines augmentent d'un montant identique il en résulte que les différentiels entre pourcentages de patrimoines initiaux diminuent, c-à-d que les patrimoines convergent vers une valeur commune, et que celle-ci vaut M/N. Les valeurs des cellules des colonnes C à E convergent vers leur correspondante de la colonne G : à la ligne 15 elles sont presque égales.
La section suivante va démontrer mathématiquement ces faits intuitifs, et n'a donc d'intérêt que pour les férus de mathématique. Elle n'apporte pas grand chose par rapport à cet énoncé, si ce n'est la réponse de Laborde à la critique de sensibilité des équations n_c=vexp(1/v)-1 ou n_c=(v/2)exp(2/v)-1 au changement d'unité.
Démonstration
Passons maintenant à la démonstration mathématique du principe de convergence des stocks monétaires relatifs. Pour ce faire Laborde recourt aux intégrales, ce qui complique la compréhension par le grand public. La version présentée ici est plus facile à comprendre.
Il s'agit de formuler la loi d'accumulation des DU dans le temps, en termes quantitatif et relatif.
On considère un utilisateur type d'un système monétaire symétrique tel que :
au moment de son entrée dans le système monétaire (nouveau né ou immigrant) il dispose d'un stock monétaire H ;
on suppose que ses revenus autres que le DU sont systématiquement compensés par des dépenses équivalentes (de sorte que seul le flux des DU qu'il reçoit régulièrement augmente son stock monétaire), ce qui revient à considérer égales les capacités de chacun à faire fructifier la rente monétaire que constitue le DU.
Quantitatif
Soit n le nombre d'années depuis lequel un individu est membre du système monétaire (n = t - t0 ⇔ t0 = t - n) alors le stock monétaire Qt de cet individu à l'instant t vaut :
Qt = H + ∑t-ntU
Si l'on suppose que la population ne varie pas c-à-d que a=0, alors puisque la création monétaire est également partagée en tous, et que c est constant, on peut écrire n_Qt=H+∑U comme suit :
Qt = H + (Mt - Mt-n ) / N ⇔
Qt = H + [ Mt - Mt / (1 + c) n ] / N ⇔
Qt = H + Mt / N * (1 - (1 + c) -n)
Si l'on observe uniquement la situation d'un individu (c-à-d qu'on ne compare pas encore la situation d'individus disposant de stocks monétaires initiaux différents) on peut poser H=0, de sorte que Qt = Mt / N * ( 1 - (1 + c) -n ). On voit alors que lim Q n→∞ = Mt / N : avec l'âge, le stock quantitatif de monnaie détenu par tout individu tend vers la masse monétaire moyenne par individu.
Relatif
Soit Rt le stock monétaire individuel exprimé relativement à la masse monétaire moyenne par individu :
Rt = Qt / (Mt / N)
En substituant n_Qt=H+Mt/N*(1-(1+c)-n) dans n_Rt=Qt/(Mt/N), c-à-d en divisant n_Qt=H+Mt/N*(1-(1+c)-n) par Mt/N on obtient :
Rt = H / (Mt / N) + 1 - (1 + c) - n
Posons à nouveau H=0 de sorte que Rt = 1 - (1 + c) -n. On voit alors que lim R n→∞ = 1, ce qui est trivial dès lors que Qt tend vers le référentiel Mt / N.
Formule simplifiée (et avec H=0) : nous avons vu que si c est suffisamment petit alors 1+ c ≈ e c n_c=eexpci-1 ⇒ sous ces conditions, n_Rt=H/(Mt/N)+1-(1+c)-n peut être reformulée comme suit :
R = 1 - e - c * n
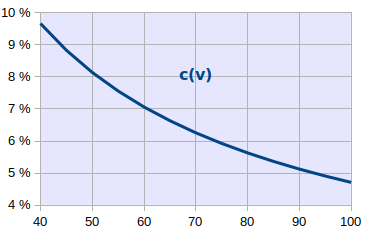
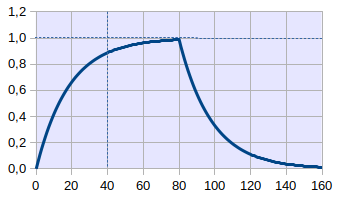
Le graphique suivant montre l'évolution de Rt durant la vie d'un individu, et simule l'effet d'un décès à 80 ans, moment à partir duquel Qt n'augmente plus de sorte que Rt diminue et tend rapidement vers zéro à la limite.
Poursuivons les développement mathématiques (avec a=0). Emmanuel Bultot [source p. 17] démontre comme suit la convergence de Rt vers zéro après la mort de l'individu à l'âge m. On veut connaître la valeur de :
n_Rt=Qt/(Mt/N) : Rm+x = Qm / [ Mm+x / N ]
où l'on substitue :
n_Qt=H+Mt/N*(1-(1+c)-n) (avec H=0) : Qm = Mm / N * [ 1 - (1 + c) -m ]
de sorte que :
Rm+x = Mm / N * [1 - (1+c) -m ] / [ Mm * (1+c) x / N ] ⇔
Rm+x = [1 - (1+c) m ] / (1+c) x
Et on a bien que lim R x→∞ = 0 puisque m est constant.
Il nous faut interrompre ici brièvement, car le graphique de R est utilisé par Laborde pour répondre à la remarque concernant la sensibilite de n_c=vexp(1/v)-1 au changement d'unité.
Proposition de résolution du problème de changement d'unité dans c = v 1/v - 1
Nous avions évoqué plus haut que c = v 1/v - 1 n_c=vexp(1/v)-1 pose problème : elle n'est pas inchangée en cas de changement d'unité (par exemple si on exprime l'année en 365 jours plutôt qu'en douze mois) : cf. #valeur-de-c.
C'est évidemment aussi le cas de c = v/2 2/v - 1 n_c=(v/2)exp(2/v)-1, version "monnaie libre" de n_c=vexp(1/v)-1.
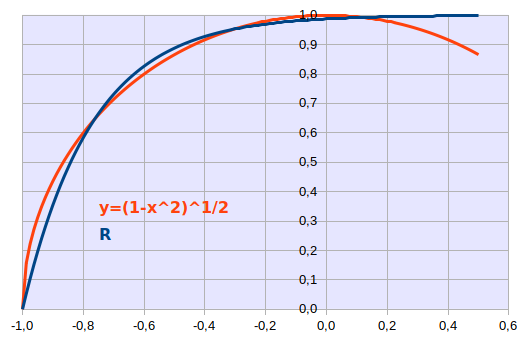
Pour trouver un formulation de c qui ne soit plus sensible au changement d'unité, Laborde propose une solution [source], qui repose sur le fait que la courbe de R, avant sa décroissance, peut être approchée par l'équation du cercle (notion de régression circulaire) : y = √ (1 - x2) (cf. théorème de Pythagore).
On procède alors en deux étapes :
- à partir de R = 1 - e - c * n n_Rt=1-e-c*n, exprimer c en fonction de R et n : c = - ln( 1 - R ) / n
- dans cette équation, remplacer n et R par leur valeur calculée, pour un point quelconque de l'équation du cercle. Dans le graphique ci-contre, nous avons normalisé cette portion de cercle, de sorte que l'année de naissance correspond à -1, et l'année d'espérance de vie à 0 ⇒ les valeurs correspondant par exemple au premier quart de l'espérance de vie (soit n=v/4) sont alors x=-3/4 ⇒ y=R=√(1-(-3/4)2)=0,66 ⇒
c = -ln(1-0,66) / v/4 = 1,1 * 4 / v ⇒
c ≈ 4 / v n_c≈4/v
où l'on a maintenant équivalence quelle que soit l'unité temporelle :- annuel : c = 4/80 = 5 %/an
- mensuel : c = 4/(80*12) = 0,4 %/mois soit 1,00412-1= 5%/an
La formule n_c≈4/v concerne la monnaie directe. Pour la monnaie libre, il suffit de remplacer v par v/2 ⇒
c ≈ 8 / v n_c≈4/v
Sur la différence entre monnaie directe et monnaie libre, cf. supra #monnaies-libres-vs-monnaie-directe
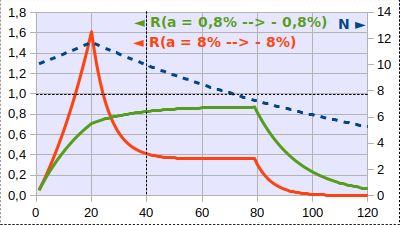
Notons enfin que cette réponse de Laborde ne vaut que si a est petit. Ainsi le graphique suivant montre l'effet sur R, de valeurs absolues de a supérieure et inférieur à c (5,6%), et changeant de signe après 20 périodes. Elle n'est donc généralement pas applicable au cas des monnaies libres ...
Patrimoines
différents
Cette digression étant terminée, revenons à nos démonstrations mathématiques (toujours avec a=0). Nous avons procédé à une analyse de Rt du point de vue d'un individu quelconque, en posant H=0. Levons maintenant cette hypothèse afin de traiter l'approche comparative entre individus de stocks monétaires initiaux différents Hi. Je reprends également ici la démonstration d'Emmanuel Bultot [source p. 18], qui pose H = h * Mt0 / N (c-à-d une proportion h de la masse monétaire moyenne par individu au moment où l'individu i entre dans le système monétaire) dans n_Rt=H/(Mt/N)+1-(1+c)-n Rt = H / (Mt / N) + 1 - (1 + c) -n ⇒
Rt = h * Mt0 / N / (Mt / N) + 1 - (1 + c) -n
= h * (Mt0 / Mt) + 1 - (1 + c) -n
= h * (1 + c) - n + 1 - (1 + c) - n ⇔
Rt = 1 + ( h - 1 ) / ( 1 + c ) n
On voit donc que – quelle que soit la valeur de h, et donc de H – lim R n→∞ = 1 c-à-d lim Q n→∞ = Mt / N. C'est là un résultat trivial que l'on pouvait déjà deviner dans Qt = H + ∑t-ntUi n_Qt=H+∑U : vu que H est constant et que les DU s'accumulent constamment, la part relative de H diminue ⇒ la valeur de Qt approche la somme des DU, or ceux-ci représentent des parts égales de ΔM.
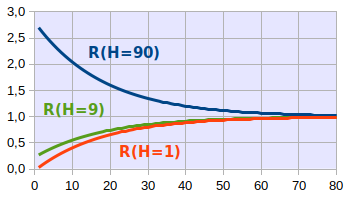
On peut visualiser facilement ce résultat en simulant une économie fictive au moyen d'un tableur. Le graphique suivant correspond à nos trois individus dont le stock monétaire de départ est respectivement de 1, 9 et 90, de sorte que la masse monétaire de départ est de 100.
L'égalité Rt = 1 + ( h - 1 ) / ( 1 + c ) n n_Rt=1+(h-1)/(1+c)n révèle que la courbe H=90 correspond à h>1 tandis que les deux autres correspondent à h<1 :
1 + ( h - 1 ) / ( 1 + c ) n > 1 ⇔
( h - 1 ) / ( 1 + c ) n > 0 ⇔
h - 1 > 0 ⇔
h > 1
Ainsi donc un système monétaire symétrique a pour effet de réduire les différentiels de stock monétaire. L'équation n_Rt=H/(Mt/N)+1-(1+c)-n montre que plus c est élevé plus rapide est la convergence. Ce fait intuitif peut être vérifié dans le tableur.
Fiscalité redistributive
Nous venons de montrer que la symétrisation du système de création monétaire – c-à-d la création monétaire à taux constant, et sa distribution égalitaire et gratuite entre les seules personnes physiques – induit un effet de limitation relative des écarts de richesse : les stocks monétaires individuels exprimés relativement à la masse monétaire moyenne par individu (Ri) convergent vers l'unité.
Par conséquent, peut-on en déduire que la symétrisation du système monétaire rendrait obsolète la nécessité de réduire les écarts de richesse via la fiscalité redistributive ?
Pas sûr... Commençons par constater que l'AUD ne représente qu'environ 200 euros/mois, soit 16 % de l'AU. Les 84 % restant correspondent à l'AUR, c-à-d à la fiscalité redistributive.
Cette répartition, assez déséquilibrée, entre les parts de financements monétaire (distributif) et fiscal (redistributif) de l'AU va-t-elle s'avérer être constante ? Ou bien va-t-elle fluctuer ? Dans ce second cas, va-t-elle fluctuer autour d'une valeur d'équilibre ? Dans l'affirmative, l'évolution vers une valeur d'équilibre va-t-elle passer par une phase de compensation de la non application historique du principe de symétrie spatio-temporelle à la création & allocation monétaire ? Quelle voie emprunterait cette compensation : fiscale ou monétaire ?
D'autre part, une éventuelle valeur d'équilibre des parts AUD et AUR correspondrait-elle au concept d'écart de richesse optimal (cf. /production.php#ecart-richesse-optimal) ?
Il n'est pas facile de répondre à toutes ces questions, car les modes de production d'une économie fondée sur notre AU seront très différents de ce qu'ils sont aujourd'hui.
Voilà qui nous conduit à la notion de champ de valeurs, notion mathématique par laquelle Laborde introduit la notion de développement durable dans la TRM.
Champ de valeurs économiques
2. Formulation
Principes
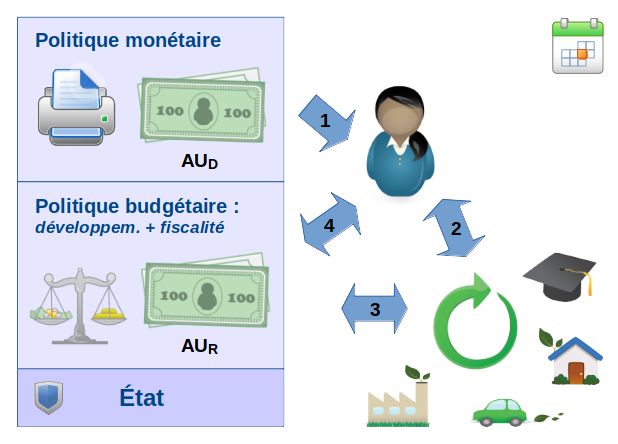
Si l'État était véritablement sous contrôle démocratique il pourrait alors décider que la création monétaire doit être injectée dans l'économie, non plus via les banques commerciales (personnes morales), mais directement via les citoyens (personnes physiques), en répartissant la création monétaire gratuitement et également entre eux.
Cette méthode est bien plus rationnelle que d'allouer la création monétaire via des prêts bancaires, c-à-d des sommes créées ex-nihilo, et pourtant prêtées avec obligation de remboursement du principal, et de paiement d'un intérêt s'ajoutant au principal. Rappelons à cet égard que ces prêts sont accordés de façon discrétionnaire par les banques commerciales, non pas pour maximiser le bien-être collectif mais pour maximiser leurs bénéfices !
Or ce ne sont pas les banques mais les citoyens – clients ultimes de l'économie, mais aussi producteurs locaux – qui par leurs achats et productions locales, sont les mieux à même d'indiquer à l'État et aux grandes entreprises quels types d'investissements celles-ci devraient réaliser pour participer efficacement à la production de produits et services utiles à la collectivité et respectueux de l'environnement (infrastructures, etc).
Ainsi la structure productive de nos économies serait bien plus efficace car développée, non plus en fonction des intérêts de cette infime minorité de la population que sont les principaux actionnaires des banques, mais bien en fonction des besoins de la majorité de la population. Il en résulterait une meilleure adéquation de l'offre à la demande de biens et services, et par conséquent une plus grande stabilité économique.
En outre l'impact écologique serait particulièrement bénéfique. En effet, dans le système économique actuel – sans allocation universelle telle que définie par le modèle synthétique – les populations pauvres convergent vers les zones de concentration du capital (capitalisme). La contrepartie de l'exode rurale c'est l'uniformisation des paysages par des méga-entreprises (agricoles dans les campagnes, industrielles dans les villes), ainsi que l'évincement de l'artisanat et des productions locales.
Un système monétaire symétrique (création monétaire à taux constant, et distribution gratuite et égalitaire entre les seules personnes physiques) inverserait le processus : ce ne sont plus les individus qui devraient se déplacer vers le capital (migration ou navettage), mais au contraire celui-ci qui serait réparti vers les individus là où ils habitent. Ainsi en opérant une meilleure répartition géographique du capital le système monétaire participerait à :
- éradiquer les zones de sur-concentration de production/consommation, ainsi que les méga-entreprises qui tuent l'artisanat et la production locale ;
- réduire le volume des navettages quotidiens pour se rendre à son lieu de travail.
On voit donc que l'AU permet le financement direct des circuits courts (production et consommation locales), c-à-d l'autosuffisance régionale, moins polluante que le modèle des méga-hub de production et de distribution qui implique le transport des marchandises sur de plus longues distances, augmentant ainsi la pollution et le réchauffement climatique. Autre conséquence importante de cette décentralisation des capacités de production : un système économique plus résilient.
Un système monétaire symétrique constitue donc un élément essentiel du développement durable.
Formulation
Selon Laborde l'égalité M * V = P * Q (pour approfondir cette équation fondamentale de la théorie quantitative de la monnaie, voir notre article "Principes monétaires") ne concerne que des quantités "intégrales globales" et n'est valable que « pour un temps court où les changements productifs, monétaires et individuels sont négligeables » . Dans la réalité cette situation où la monnaie en circulation représente exactement la valeur produite et échangée se produit rarement, de sorte que l'on a plutôt
M * V - P * Q = Jt
où Jt – différentiel "monnaie-valeur" – est appelé « champ de valeurs J à l'instant t ». Sa valeur pouvant être positive, négative ou nulle, l'égalité de la théorie classique M * V = P * Q n'est donc, dans la théorie relativiste, que le cas particulier (et rare) où Jt = 0.
Ceci est à rapprocher de la théorie thermodynamique de l'économie développée notamment par le physicien François Roddier, et dont nous avons montré qu'elle conduit à définir V (vitesse de circulation monétaire) comme l'inverse du potentiel de demande (utilité de la production) : une vitesse de circulation monétaire croissante "consomme" le potentiel de demande. On notera également la proximité entre l'équation M * V - P * Q = Jt et la relation de Gibbs-Duhem, le cas particulier où Jt = 0 correspondant à une situation dite "d'état stationnaire" caractérisée par une pression et température constantes. Mais le phénomène économique est plutôt caractérisé par un état d'équilibre instable où la valeur de Jt oscille autour de zéro.
La modélisation proposée par Laborde :
- procède par l'intégration des champs de valeurs locaux associés à chaque individu x (notés dJx) ;
- distingue production et échanges.
Mathématiquement le champ de valeurs Jt est ainsi formulé par l'intégrale des champs différentiels :
Jt = ∫ t0t∑x=1ndJx
où dJx =
( dMpx + dMex ) - ( Ppx * dQpx + Pex * dQex )
forme "Monnaie - Valeur"( dMpx - Ppx * dQpx ) + ( dMex - Pex * dQex )
forme "ΔProduction + ΔÉchange"
où :
- dMpx : monnaie produite au niveau de l'individu x (c-à-d le dividende universel U) ;
- dMex : de la monnaie échangée (> 0 ou < 0) par l'individu x ;
- Ppx * dQpx : potentiel de production de valeur par l'individu x [1] ;
- Pex * dQex : valeur échangée (> 0 ou < 0) par l'individu x avec le reste du monde.
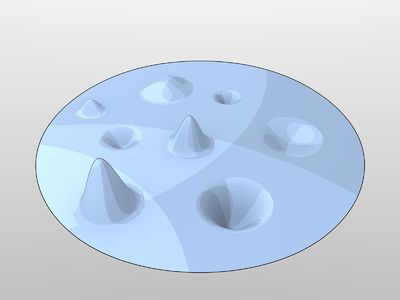
Géométriquement le champ de valeurs est donc composés de "bosses" (dJx > 0) et de "creux" (dJx < 0). Les bosses sont des zones locales où il y a « surplus de monnaie par rapport à la valeur potentielle de la production locale effective de biens et services ». Les creux sont des zones où la valeur potentielle de la production locale excède la quantité de monnaie présente dans la zone. La TRM formalise ainsi de façon rigoureuse la dynamique des phénomènes d'instabilité évoqués plus haut : spéculation financière, exode rural, délocalisations d'entreprises, désindustrialisation, inflation/déflation, ...
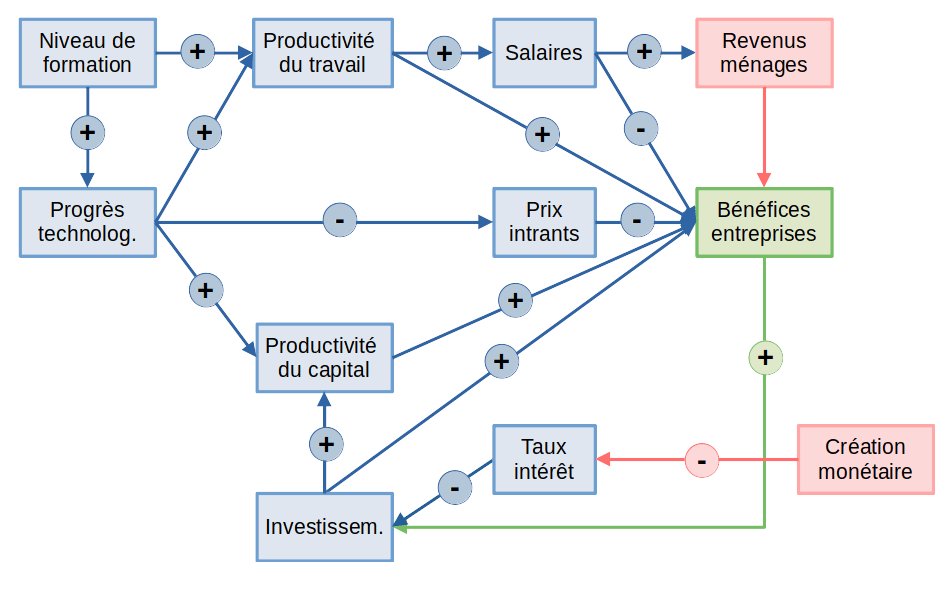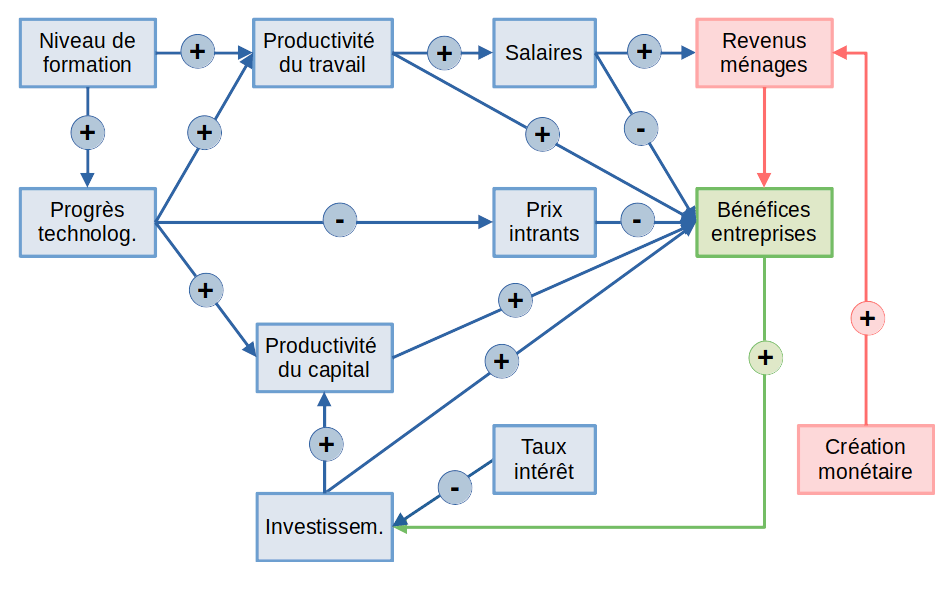
• Lecture de la ligne horizontale centrale : le progrès technologique tend à réduire le prix des matières premières, ce qui augmente le bénéfice de entreprises.
• Lecture des colonnes : colonne 2 : productivités des facteurs de production, colonne 3 : coût des facteurs de production, colonne 4 : revenus des agents économiques privés.
Pour approfondir :
- réfutations des arguments du secteur bancaire "justifiant" que la création de monnaie lui soit attribuée : /creation-monetaire#allocation-monetaire ;
- notre analyse spatio-temporelle de l'inflation : /principes-monetaires#formation-des-prix.
Le concept de champ de valeurs étant défini, abordons maintenant la question du rapport entre TRM et inflation.
Affichage des prix en DU
2. Pouvoir d'achat
3. Effet sur la croissance
Relativité des prix
Laborde attire notre attention sur la relativité des prix, et plus particulièrement sur deux caractéristiques :
on peut exprimer les prix dans n'importe quel référentiel, par exemple exprimer des tomates en concombres ou en DU (dividende universel) plutôt qu'en euros ;
le prix d'un bien peut augmenter dans un référentiel, tout en diminuant dans un autre; on le constate tous les jours avec les devises (qui sont aussi des biens) : une devise A s'apprécie par rapport à une devise B, alors que dans le même temps elle se déprécie par rapport à une devise C.
On notera que cette relativité des prix concerne le troc en général. "Prix relatif" est synonyme de "valeur d'échange".
Dans le cas de monnaies on parle de pouvoir d'achat plutôt que de valeur d'échange.
Évoquant alors les quatre "libertés" de la monnaie libre (cf. infra), l'auteur de la TRM nous rappelle notre droit d'exprimer les prix dans le référentiel de notre choix. Formidable, mais quelle en est l'utilité ? Si chaque vendeur exprime ses prix de vente dans le référentiel de son choix la monnaie ne perd-elle pas de son efficacité en tant qu'instrument d'échange ainsi que de comptabilité ? Comprenons bien qu'exprimer le prix relativement à n'importe quel autre, ça n'est rien d'autre que le troc ...
Exprimer les prix en DU. Laborde propose d'exprimer les prix relativement au DU, qui ferait ainsi fonction de référentiel relativiste.
Notons cependant que le DU n'est pas un invariant relativiste puisque Ut = c * Mt-1 / Nt n_Ut=c*Mt-1/Nt, contrairement à Ut / ( Mt / Nt ) = c / ( 1 + c ) n_Ut/(Mt/Nt)=c/(1+c).
Une intuition implicite est que cet affichage relativiste des prix ferait d'autant plus sens (i) que la masse monétaire serait créée à taux constant (symétrie temporelle), et (ii) que cette création monétaire serait partagée également entre toutes les personnes physiques (symétrie spatiale).
Notons enfin une conséquence importante de l'affichage des prix en DU : cela garantirait aux vendeurs de recevoir toujours le même pouvoir d'achat lors de la vente, dès lors que, abstraction faite de l'inflation non monétaire, le prix exprimerait toujours la même part de la création monétaire.
Thermoéconomie. Il est intéressant à cet égard de noter l'approche de François Roddier, physicien converti à la thermoéconomie : « Par analogie avec les fluides, nous avons défini la température d’une économie comme étant l’énergie dissipée par unité monétaire. On peut, de même, définir la température d’une société comme étant l’énergie qu’elle dissipe par bit d’information mémorisée. Dans ce qui suit, nous supposerons fixe le coût de l’énergie. C’est ce qui se passe si on indexe la monnaie sur l’énergie disponible, ce qu’il faudrait faire pour une monnaie internationale comme l’Euro. On peut alors mesurer l’énergie en Euros (son coût) et examiner le rôle de l’information autre que monétaire » [source].
Pouvoir d'achat
La valeur d'échange de la monnaie c-à-d son pouvoir d'achat peut être mesuré par la quantité de biens et services que l'on peut acheter avec une unité de monnaie, soit Q/M. Par conséquent il ressort de l'égalité de Fisher que Q / M = V / P, c-à-d que :
- V/P est une mesure du pouvoir d'achat de la monnaie ;
- à Q et V constants, le pouvoir d'achat de la monnaie diminue si M ou P augmente ;
- à M constant, si Q augmente (gain de productivité ou augmentation de la population) le pouvoir d'achat de cette monnaie augmente.
Il convient cependant d'interpréter prudemment l'égalité de Fisher. Pour s'en rendre compte lire notre critique de la thèse de neutralité de la monnaie : /principes-monetaires#neutralite.
D'autre part ne perdons pas de vue que l'égalité de Fisher ne représente pas la réalité, car elle ne concerne que l'aspect quantitatif de la théorie monétaire, faisant abstraction de la dimension qualitative, en particulier le mode d'allocation de la création monétaire entre agents économiques (cf. supra la notion de champ de valeurs). Autrement dit, l'égalité de Fisher ne décrit pas une loi de la nature économique mais un type de système monétaire, caractérisé par la monnaie-crédit.
Approfondissons maintenant l'analyse des effets d'un affichage des prix en DU. Que se passerait-il si tous les prix, y compris ceux du travail (les salaires), étaient exprimés en DU ?
Effet sur la croissance
Supposons que les "étiquettes" affichant les prix des biens et services (marchandises et salaires) sont connectées par wifi en temps réel à la comptabilité de la Banque centrale, et les prix indexés en temps réel sur la masse monétaire. Quel serait l'impact d'une telle indexation sur le taux d'inflation (i) et sur la croissance économique (g) ?
La réponse de la théorie quantitative de la monnaie est donnée par l'égalité de Fisher M * V = P * Q) exprimée en taux de croissance c ≈ i + g (V est assez stable pour M3).
On obtient alors deux options théoriques selon que l'on considère que l'inflation est ou n'est pas un phénomène d'origine exclusivement monétaire :
l'inflation est exclusivement d'origine monétaire --> i' = c --> g' ≈ 0 ⇔ l'indexation des prix sur M rend impossible la croissance économique ;
l'inflation n'est pas que d'origine monétaire --> i' > i (puisque la croissance monétaire serait immédiatement et intégralement transformée en inflation) --> g' = c - i' < g = c - i ⇔ l'indexation des prix sur M freine la croissance économique.
Mais qu'en serait-il si plutôt que d'indexer les prix sur la masse monétaire, nous exprimions ceux-ci en fonction du DU ?
l'inflation est exclusivement d'origine monétaire --> i' = 0 --> g' ≈ c ⇔ exprimer les prix en DU stabilise la croissance économique ;
l'inflation n'est pas que d'origine monétaire --> i' < i (puisque l'inflation mesurée ne serait plus que non monétaire) --> g' = c - i' > g = c - i ⇔ exprimer les prix en DU stimule la croissance économique.
On arrive au même résultat en partant de (17) M * V - P * Q = Jt qui est l'égalité de Fisher version TRM. Posons Jt égal à une proportion aléatoire kt de la masse monétaire, telle que -0,5 < kt < 0,5 :
Jt = kt * Mt ⇔
Mt * Vt - Pt' * Qt = kt * Mt ⇔
Mt * ( Vt - kt ) = Pt' * Qt ⇔
ce qui exprimé en taux de croissance donne :
c = i' + g (V est relativement stable pour M3, et k est aléatoire).
On a raisonné ici au niveau macroéconomique, mais qu'en est-il au niveau microéconomique ? Observant le prix du mètre carré à Paris entre 1995 et 2015 et en le comparant au RSA, Laborde observe que ces prix varient moins si on les mesure par rapport au RSA [source]. Mais ce résultat est trivial, il n'apporte rien au niveau théorique. En effet, soit P le niveau de prix et U le DU, i et c leurs taux de croissance respectifs, si on divise P par U on a évidemment que P / U < P ⇒ i - c < i (pour i et c petits, ce qui est généralement vérifié).
La réflexion originelle – à savoir le fait que la valeur d'un bien A (une pomme, un logiciel, une devise, ...) peut s'apprécier par rapport à celle d'un bien B, et dans le même temps se déprécier par rapport à un bien C – est intéressante car elle pose le problème de la valeur d'un même bien exprimée dans deux devises différentes, ou encore le pouvoir d'achat d'une même devise dans deux pays où les niveaux des prix ne sont pas identiques. Nous allons donc dans les sections suivantes nous intéresser à l'inflation et aux taux de change sous l'angle de la TRM.
Inflation
Que se passerait-il si la Banque centrale d'un pays décidait brusquement d'interdire aux banques commerciales de créer de la monnaie, pour la créer elle-même, à taux constant, et la distribuer également et gratuitement entre tous les citoyens ?
En particulier qu'en deviendrait-il de la nocivité présumée de l'inflation d'origine monétaire (cf. /principes-monetaires.php#inflation-effets) dès lors que la création monétaire serait (i) à taux constant (--> pas d'erreurs d'anticipations par les agents économiques), et (ii) également partagée entre tous ? (--> moins de spéculation, structure productive mieux adaptée aux besoins de la majorité de la population).
Pour élaborer certains éléments de réponse à cette difficile question, notre analyse impliquera l'offre de travail, l'offre de monnaie, la demande et l'offre de biens & services, enfin "last but not least" la structure productive.
Offre de travail. Concernant l'impact du DU sur l'offre de travail voir notre article consacré à l'application de l'AU du modèle synthétique (soit 1250 euros/mois dont 16 % consiste en le DU), et qui montre que l'effet devrait être modéré (tout en étant souhaitable).
Offre de monnaie. D'autre part la valeur de c n'est pas significativement différente du taux historique de croissance monétaire de sorte que le risque d'inflation par la demande n'est pas significativement modifié.
Demande de biens et services. On pourrait cependant arguer que la meilleure répartition de la création monétaire va mécaniquement provoquer une forte hausse de la demande dans la sphère réelle (au détriment de celle dans la sphère financière) malgré que par rapport à la situation actuelle l'évolution de la masse monétaire ne serait pas modifiée. Il en résulterait un accroissement considérable du risque inflationniste dans la sphère réelle (là où vivent les moins riches).
Offre de biens et services. Mais d'autre part la garantie d'un effet positif récurrent de l'AU sur la demande dans la sphère réelle devrait inciter les producteurs de biens et services à utiliser une partie de la hausse des bénéfices pour investir en nouvelles capacités de production. Par conséquent le potentiel inflationniste reviendrait à son niveau initial lorsque les capacités auront été accrues.
Structure productive. Enfin n'oublions pas que la politique monétaire n'est pas que de nature quantitative (création monétaire) : elle est également qualitative (allocation monétaire). Or la section supra consacrée au champ de valeurs suggère que si la création monétaire était désormais distribuée gratuitement et également entre tous les citoyens cela modifierait considérablement la problématique inflationniste.
Comprenons bien que nous comparons ici "des pommes avec des poires", ou plutôt des pommes d'hier avec des pommes de demain. Si notre système monétaire avait toujours été symétrique notre structure productive (quelles régions produisent quoi, et en quelles quantités ?) serait aujourd'hui très différente car elle aurait été développée non plus en fonction des intérêts de cette infime minorité de la population que sont les principaux actionnaires des banques, mais bien en fonction des besoins de la majorité de la population --> meilleure adéquation de l'offre à la demande de biens et services --> moins de périodes d'inflation et de déflation. En outre, en raison de l'effet de convergence, les écarts de richesse --> les bulles spéculatives à répétition --> les subséquentes crises économiques auraient été de moindre ampleur ou moins fréquentes.
Ainsi les simulations réalisées au moyen du jeu Ğconomicus, qui comparent l'activité économique dans un système monétaire asymétrique avec l'activité en système symétrique (libre ou direct), montrent que dans le second cas les échanges économiques (le PIB) sont supérieurs, et les écarts de richesse inférieurs [source].
Taux de change
Les développements présentés jusqu'ici concernaient une seule zone économique indépendamment des autres (chacune correspondant à une espérance de vie et une monnaie spécifique). Dans la réalité des zones monétaires différentes sont en relation et échanges des biens et services contre des devises. Que dit la TRM concernant le taux de change entre devises symétriques ?
Une zone monétaire
une durée de vie
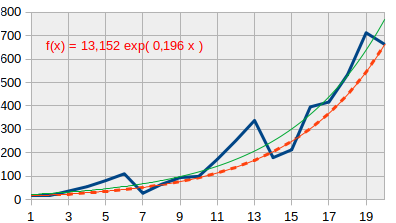
L'équation c ≈ 4 / v n_c≈4/v, illustrée dans le graphique ci-dessous, montre que le principe de symétrie spatio-temporelle requiert que c soit plus élevé dans les zone économiques dont l'espérance de vie est plus faible, ou encore qu'il baisse lorsque l'espérance de vie d'une zone économique augmente.
Il y a là cohérence avec le fait que taux de croissance économique est généralement plus élevé dans les pays moins développés que dans les pays plus développés.
Taux de change
théorique (TRM)
J'ai trouvé le texte de Laborde sur ce point peu explicite voire confus. La présente section a pour objet d'y remédier.
Si deux vaches valent trois moutons (2 * V = 3 * M) alors le cours de la vache en mouton est de 3/2 moutons (V = 3/2 * M), et le taux de change de la vache en moutons (3/2) est le nombre de moutons échangés divisé par le nombre de vaches échangées, c-à-d le nombre de moutons échangés par vache.
Généralisation. Soit eA/B le taux de change de A en B alors :
eA/B = #B / #A
Ainsi un cours de 1 EUR = 1,252 USD signifie que le taux de change de l'euro en dollars (eEUR/USD) est de 1,252 dollars par euro.
Par conséquent un taux de change théorique de la devise de masse monétaire MA en la devise de masse MB est le taux potentiel :
eA/B = MB / MA
"Potentiel" parce que le nombre total d'unités monétaires est la limite maximale du nombre d'unités échangeables.
Dans le cadre d'un système monétaire symétrique où la monnaie est créée à taux constant, l'égalité n_eA/B=MB/MA prend toute sa signification, et encore plus en y intégrant le fait que la création monétaire est distribuée également à la population (NA et NB respectivement) :
eA/B = (MB / NB) / (MA / NA)
Le tableau suivant montre que le taux de change eEUR/USD théorique relativiste calculé à partir de l'égalité n_eA/B=(MB/NB)/(MA/NA) est du même ordre de grandeur que le taux de change observé. Ce fait remarquable confirme la pertinence de cette valeur théorique.
| EEUR/USD | Valeur (2010) |
|---|---|
| Théorique | 1,60 |
| Observé | 1,25 - 1,45 |
Et là encore il convient de faire la même remarque que pour l'inflation : on compare ici des pommes et des poires, ou plutôt des pommes d'aujourd'hui avec des pommes d'hier. Le concept de champ de valeurs développé plus haut suggère en effet que si notre système monétaire avait toujours été symétrique notre structure productive (quelles régions produisent quoi et en quelles quantités ?) serait aujourd'hui très différente car elle aurait été développée non plus en fonction des intérêts de cette infime minorité de la population que sont les actionnaires des banques, mais bien en fonction des besoins de la majorité de la population --> meilleure adéquation de l'offre à la demande de biens et services --> moins de périodes d'inflation et de déflation. En outre, en raison de l'effet de convergence (cf. égalité 21), les écarts de richesse --> les bulles spéculatives à répétition --> les subséquentes crises économiques auraient été de moindre ampleur ou moins fréquentes.
Pour une comparaison de la TRM avec la théorie classique des taux de change voir : /principes-monetaires#determinants-des-taux-de-change
[1] La notion de potentialité exprime ici le fait que de nombreux échanges ou productions ne sont pas monétisés au moment où ils se produisent. Laborde cite comme exemple le cas de Richard Stallman – initiateur du mouvement du logiciel libre – qu'il considère comme un des plus grands créateurs de valeur économique ayant jamais existé mais qui pourtant n'en a retiré quasiment aucun bénéfice.